Inscribed angle theorem of Right triangle Problems - last page
Number of problems found: 25
- Circular pool
The pool's base is a circle with a radius r = 10 m, excluding a circular segment that determines the chord length of 10 meters. The pool depth is h = 2m. How many hectoliters of water can fit into the pool? - Circle inscribed
Calculate the perimeter and area of a circle inscribed in a triangle measuring 3, 4, and 5 cm. - The chord
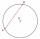A chord passing through its center is the side of the triangle inscribed in a circle. What size are a triangle's internal angles if one is 40°? - Circle section
An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a - Semicircle
The semicircle with center S and the diameter AB is constructed equilateral triangle SBC. What is the magnitude of the angle ∠SAC?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
