Perimeter of Angle Problems - page 5 of 6
Number of problems found: 110
- Ratio in trapezium
The ratio of the height v and the base a, c in the trapezoid ABCD is 1:6:3. Its area is 324 square cm, and the peak angle B is 35 degrees. Determine the perimeter of the trapezoid. - Circular railway
The railway connects points A, B, and C in a circular arc, whose distances are | AB | = 30 km, AC = 95 km, and BC | = 70 km. How long will the track be from A to C? - Disc
The circumference of the disk is 78.5 cm. What is the circumference of the circular arc of 32° on the disc? - Triangle SAS
Calculate the triangle area and perimeter if the two sides are 46 m and 33 m long and angle them clamped is 170 °. - Trapezoid MO
The rectangular trapezoid ABCD with the right angle at point B, |AC| = 12, |CD| = 8, diagonals are perpendicular to each other. Calculate the perimeter and area of the trapezoid. - Triangle - many properties
In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an - Nonagon
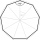Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm.
- Quadrilateral 42151
Calculations from geometry: The ratios of the sides of the quadrilateral are 3 : 6:4.5 : 3.5. Calculate their lengths if the circumference is 51 cm. The sizes of the angles in the quadrilateral are equal to 29°30', 133°10', and 165°20'. What is the size o - Rectangular trapezoid
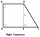The ABCD rectangular trapezoid with the AB and CD bases is divided by the diagonal AC into two equilateral rectangular triangles. The length of the diagonal AC is 62cm. Calculate the trapezium area in cm square and calculate how many different perimeters - Rectangular trapezoid
The rectangular trapezoid ABCD is: /AB/ = /BC/ = /AC/. The length of the median is 6 cm. Calculate the circumference and area of a trapezoid. - Circle arc
The circle segment has a circumference of 135.26 dm and 2096.58 dm² area. Calculate the radius of the circle and the size of the central angle. - In plane 2
A triangle ABC is located in the plane with a right angle at vertex C, for which the following holds: A(1, 2), B(5, 2), C(x, x+1), where x > -1. a) determine the value of x b) determine the coordinates of point M, which is the midpoint of line segment - Determine 19953
The distance between the tip of the minute hand and the center of the dial is 12 mm. Determine the distance traveled by the tip in 45 min. (draw a clock face and a minute hand and realize the distance it will cover in 45 min.) - Circular segment
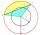Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ) - Hexagon in circle
Calculate the radius of a circle whose length is 10 cm greater than the circumference of a regular hexagon inscribed in this circle.
- The amphitheater
The amphitheater has the shape of a semicircle, the spectators sit on the perimeter of the semicircle, and the stage forms the diameter of the semicircle. Which spectators, P, Q, R, S, and T, see the stage at the greatest viewing angle? - As shown
As shown, in △ ABC, ∠C = 90°, AD bisects ∠BAC, DE⊥AB to E, BE = 2, BC = 6, then the perimeter of △ BDE - Spectators 7562
The theater has the shape of a semicircle, and the podium is the diameter of a semicircle. Spectators K, L, M, N, and O, sit around the perimeter. Who sees the podium at the greatest angle? - Three
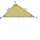Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle - Isosceles 67744
Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle.
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
Perimeter - practice problems. Angle practice problems.
