Pythagorean theorem + circular sector - practice problems
Number of problems found: 21
- Bridge
 The bridge arc has a span of 159 m and a height of 14 m. Calculate the radius of the circle arc of this bridge.
The bridge arc has a span of 159 m and a height of 14 m. Calculate the radius of the circle arc of this bridge. - Chord - TS v2
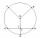 The radius of circle k measures 72 cm. Chord GH = 11 cm. What is TS?
The radius of circle k measures 72 cm. Chord GH = 11 cm. What is TS? - The circle arc
 Calculate the span of the arc, which is part of a circle with diameter d = 11 m and its height is 5 m.
Calculate the span of the arc, which is part of a circle with diameter d = 11 m and its height is 5 m. - Pendulum
 Calculate the pendulum's length 2 cm lower in the lowest position than in the highest position. The circular arc length to be described when moving is 20cm.
Calculate the pendulum's length 2 cm lower in the lowest position than in the highest position. The circular arc length to be described when moving is 20cm. - Diameter 5668
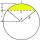 The span of the arc is 247 cm, and the height of the arc is 21.5 cm. What is the diameter of the circle?
The span of the arc is 247 cm, and the height of the arc is 21.5 cm. What is the diameter of the circle? - A goat
 In the square garden of side (a), a goat is tied in the middle of one side. Calculate the length of the rope (r) so that the goat grazes exactly half the garden. If r = c * a, find the constant c.
In the square garden of side (a), a goat is tied in the middle of one side. Calculate the length of the rope (r) so that the goat grazes exactly half the garden. If r = c * a, find the constant c. - Flakes
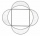 A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips?
A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips?
- Circle section
 An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a
An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a - Quarter circle
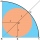 What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm?
What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm? - The tower
 The tower of the Dean's Church in Ústí nad Labem deviates from the original vertical axis by 220 cm. Its original height was 48 m. At what height is the highest point of this tower now? Enter the result to the nearest centimeter.
The tower of the Dean's Church in Ústí nad Labem deviates from the original vertical axis by 220 cm. Its original height was 48 m. At what height is the highest point of this tower now? Enter the result to the nearest centimeter. - Circular segment
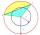 Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ)
Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ) - Lunes of Hippocrates
 Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the
Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the - MO SK/CZ Z9–I–3
 John had the ball that rolled into the pool and swam in the water. Its highest point was 2 cm above the surface. The circle's diameter that marked the water level on the ball's surface was 8 cm. Find the diameter of John's ball.
John had the ball that rolled into the pool and swam in the water. Its highest point was 2 cm above the surface. The circle's diameter that marked the water level on the ball's surface was 8 cm. Find the diameter of John's ball. - Cone A2V
 The cone's surface in the plane is a circular arc with a central angle of 126° and an area of 415 cm². Calculate the volume of a cone.
The cone's surface in the plane is a circular arc with a central angle of 126° and an area of 415 cm². Calculate the volume of a cone. - Sphere parts, segment
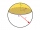 A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. What are the volume and surface of the segment?
A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. What are the volume and surface of the segment?
- Volume of the cone
 Calculate the cone's volume if its base area is 78.5 cm² and the shell area is 219.8 cm².
Calculate the cone's volume if its base area is 78.5 cm² and the shell area is 219.8 cm². - Surface of the cone
 Calculate the cone's surface if its height is 8 cm and the volume is 301.44 cm³.
Calculate the cone's surface if its height is 8 cm and the volume is 301.44 cm³. - A spherical segment
 The aspherical section, whose axial section has an angle of j = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the cut surface.
The aspherical section, whose axial section has an angle of j = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the cut surface. - Calculate 32321
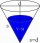 The shell of the cone is 62.8 cm². Calculate the side length and height of this cone if the diameter of the base is 8 cm.
The shell of the cone is 62.8 cm². Calculate the side length and height of this cone if the diameter of the base is 8 cm. - Maximum of volume
 The shell of the cone is formed by winding a circular section with a radius of 1. For what central angle of a given circular section will the volume of the resulting cone be maximum?
The shell of the cone is formed by winding a circular section with a radius of 1. For what central angle of a given circular section will the volume of the resulting cone be maximum?
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
The Pythagorean theorem is the base for the right triangle calculator. Pythagorean theorem - practice problems. Circular sector practice problems.
