Quadratic Equations Problems - page 28 of 30
Number of problems found: 600
- Rectangle - sides
A rectangle has an area 340 cm². The length of the shorter side is 3 cm fewer than the length of the longer side. What is the perimeter of a rectangle? - Swimming pool
The pool shape of a cuboid is 299 m³, full of water. Determine the dimensions of its bottom if the water depth is 282 cm, and one bottom dimension is 4.7 m greater than the second. - Column
The vertical pole high 7 m tall broke, and its toe fell 4.7 m from the bottom of the pole. At what height above the ground does the pole break? - Rhombus
The rhombus with area 95 has one diagonal that is longer by 7 than the second one. Calculate the length of the diagonals and rhombus sides. - Circle chord
Determine the circle's radius in which the chord 6 cm away from the center is 12 cm longer than the circle's radius. - Tubes
Iron tubes in the warehouse are stored in layers so that each tube's top layer fits into the gaps of the lower layer. How many layers are needed to deposit 100 tubes if the top layer has 9 tubes? How many tubes are in the bottom layer of tubes? - Built-up area
John build-up area 4.3 x 6.3 = 27.09 m² with building with a wall thickness 25 cm. How many centimeters would he have to subtract from the thickness of the walls that the built-up area fell by 5%?
- Tank
In the middle of a cylindrical tank with a bottom diameter of 479 cm, there is a standing rod 34 cm above the water surface. If we bank the rod, its end reaches the water's surface just by the tank wall. How deep is the tank? - Pure quadratic equation
Solve pure quadratic equation -7x² +4 = 0. - RT and circles
Solve the right triangle if the radius of the inscribed circle is r=9 and the radius of the circumscribed circle is R=26. - Rhombus and inscribed circle
It is given a rhombus with side a = 6 cm and the inscribed circle r = 2 cm radius. Calculate the length of its two diagonals. - Square Number
If to a square of integer number add 43, we get the square of the following integer number. What is the original number? - Circle
The circle touches two parallel lines, p, and q, and its center lies on line a, which is the secant of lines p and q. Write the equation of the circle and determine the coordinates of the center and radius. p: x-10 = 0 q: -x-19 = 0 a: 9x-4y+5 = 0 - Discriminant
Determine the discriminant of the equation: 3x²+19=4 - Root
The root of the equation (x-10)² +4 = x² +35x is (equal or greater or less than zero). ...
- Circle
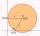Write the equation of a circle that passes through the point [0,6] and touches the X-axis point [5,0]: (x-x_S)²+(y-y_S)²=r² - Garden
The square garden area is 2/9 of a triangle garden with sides 160 m, 100 m, and 100 m. How many meters of fencing are needed to fence a square garden? - Sequence The arithmetic sequence is given: Sn=1656, d=6, an=138 Calculate a1 and n.
- Similarity
The area of the regular 10-gon is 563 cm². The area of similar 10-gon is 606 dm². What is the coefficient of similarity? - Coins
Edmund had saved a certain number of 2-euro coins. He placed the coins in a single layer in a square. He had 6 coins left. When he wanted to build a square with one more row, he was missing 35 coins. How many euros does he have?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
Are you looking for help with calculating roots of a quadratic equation?
