Similarity of triangles + angle - practice problems
Number of problems found: 60
- Observation 82811
 From the 40 m high observation deck, you can see the top of the poplar at a depth angle of 50*10' and the bottom of the poplar at a depth angle of 58*. Calculate the height of the poplar.
From the 40 m high observation deck, you can see the top of the poplar at a depth angle of 50*10' and the bottom of the poplar at a depth angle of 58*. Calculate the height of the poplar. - Mast angles and height
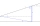 Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast.
Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast. - Right-angled 80745
 The area of a right-angled triangle KLM with a right angle at the vertex L is 60 mm square, and its hypotenuse k is 10 mm long. Triangles KLM and RST are similar. The similarity ratio is k=2.5. Calculate the area of triangle RST.
The area of a right-angled triangle KLM with a right angle at the vertex L is 60 mm square, and its hypotenuse k is 10 mm long. Triangles KLM and RST are similar. The similarity ratio is k=2.5. Calculate the area of triangle RST. - Shadow 73354
 How long is the shadow of a tree 7.6 m high, and the shadow of a 190 cm high road sign is 3.3 m long?
How long is the shadow of a tree 7.6 m high, and the shadow of a 190 cm high road sign is 3.3 m long?
- Isosceles 67744
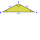 Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle.
Two isosceles triangles have the same angle at the vertex opposite the base. The first one has a base of 12 cm and a leg of 9 cm. The other has a 16 cm long base. Calculate the perimeter of the second triangle. - Three
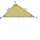 Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle
Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle - The truncated
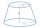 The truncated rotating cone has bases with radii r1 = 8 cm, r2 = 4 cm and height v = 5 cm. What is the volume of the cone from which the truncated cone originated?
The truncated rotating cone has bases with radii r1 = 8 cm, r2 = 4 cm and height v = 5 cm. What is the volume of the cone from which the truncated cone originated? - Tower's view
 From the church tower's view at the height of 65 m, the top of the house can be seen at a depth angle of alpha = 45° and its bottom at a depth angle of beta = 58°. Calculate the height of the house and its distance from the church.
From the church tower's view at the height of 65 m, the top of the house can be seen at a depth angle of alpha = 45° and its bottom at a depth angle of beta = 58°. Calculate the height of the house and its distance from the church. - MO Z7–I–6 2021
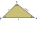 In triangle ABC, point D lies on the AC side and point E on the BC side. The sizes of the angles ABD, BAE, CAE, and CBD are 30°, 60°, 20°, and 30°, respectively. Find the size of the AED angle.
In triangle ABC, point D lies on the AC side and point E on the BC side. The sizes of the angles ABD, BAE, CAE, and CBD are 30°, 60°, 20°, and 30°, respectively. Find the size of the AED angle.
- Distance of points
 A regular quadrilateral pyramid ABCDV is given, in which edge AB = a = 4 cm and height v = 8 cm. Let S be the center of the CV. Find the distance of points A and S.
A regular quadrilateral pyramid ABCDV is given, in which edge AB = a = 4 cm and height v = 8 cm. Let S be the center of the CV. Find the distance of points A and S. - Inclined plane
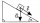 The body stays on an inclined plane and exerts a compressive force of 70N on it. Find the angle between the inclined plane and the horizontal if a gravitational force of 100N acts on the body.
The body stays on an inclined plane and exerts a compressive force of 70N on it. Find the angle between the inclined plane and the horizontal if a gravitational force of 100N acts on the body. - The triangles
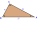 The triangles ABC and A'B'C 'are similar, with a similarity coefficient of 2. The angles of the triangle ABC are alpha = 35° and beta = 48°. Determine the magnitudes of all angles of triangle A'B'C '.
The triangles ABC and A'B'C 'are similar, with a similarity coefficient of 2. The angles of the triangle ABC are alpha = 35° and beta = 48°. Determine the magnitudes of all angles of triangle A'B'C '. - Right-angled 27683
 Right-angled triangle XYZ is similar to triangle ABC, which has a right angle at the vertex X. The following applies a = 9 cm, x=4 cm, x =v-4 (v = height of triangle ABC). Calculate the missing side lengths of both triangles.
Right-angled triangle XYZ is similar to triangle ABC, which has a right angle at the vertex X. The following applies a = 9 cm, x=4 cm, x =v-4 (v = height of triangle ABC). Calculate the missing side lengths of both triangles. - An observer
 An observer standing west of the tower sees its top at an altitude angle of 45 degrees. After moving 50 meters to the south, he sees its top at an altitude angle of 30 degrees. How tall is the tower?
An observer standing west of the tower sees its top at an altitude angle of 45 degrees. After moving 50 meters to the south, he sees its top at an altitude angle of 30 degrees. How tall is the tower?
- Approximately 25381
 The observer sees the tops of two trees at the same angle a. It is 9 m from one tree and 21 m from the other. The trees stand on a level. How tall is the second tree if the height of the first is 6 m? Remember that the eyes of a standing person are approx
The observer sees the tops of two trees at the same angle a. It is 9 m from one tree and 21 m from the other. The trees stand on a level. How tall is the second tree if the height of the first is 6 m? Remember that the eyes of a standing person are approx - The shadow
 The shadow of a 1 m high pole thrown on a horizontal plane is 0.8 m long. At the same time, the shadow of a tree thrown on a horizontal plane is 6.4 m. Determine the height of the tree.
The shadow of a 1 m high pole thrown on a horizontal plane is 0.8 m long. At the same time, the shadow of a tree thrown on a horizontal plane is 6.4 m. Determine the height of the tree. - Distance 11711
 The observer sits in a room 2 m from a 50 cm wide window. A road runs parallel at a distance of 500 m. What is the cyclist's average speed on this road when the observer sees him at 15 s?
The observer sits in a room 2 m from a 50 cm wide window. A road runs parallel at a distance of 500 m. What is the cyclist's average speed on this road when the observer sees him at 15 s? - The chimney
 The chimney casts a shadow 45 meters long. The one-meter-long rod standing perpendicular to the ground has a shadow 90 cm long. Calculate the height of the chimney.
The chimney casts a shadow 45 meters long. The one-meter-long rod standing perpendicular to the ground has a shadow 90 cm long. Calculate the height of the chimney. - Lighthouse
 Marcel (point J) lies in the grass and sees the top of the tent (point T) and, behind it, the top of the lighthouse (P). | TT '| = 1.2m, | PP '| = 36m, | JT '| = 5m. Marcel lies 15 meters away from the sea (M). Calculate the lighthouse distance from the s
Marcel (point J) lies in the grass and sees the top of the tent (point T) and, behind it, the top of the lighthouse (P). | TT '| = 1.2m, | PP '| = 36m, | JT '| = 5m. Marcel lies 15 meters away from the sea (M). Calculate the lighthouse distance from the s
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
