Triangle practice problems - page 96 of 125
Number of problems found: 2500
- Decagon prism
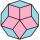 A regular decagon of side a = 2 cm is the base of the perpendicular prism. The side walls are squares. Find the prism volume in cm³, round to two decimal places.
A regular decagon of side a = 2 cm is the base of the perpendicular prism. The side walls are squares. Find the prism volume in cm³, round to two decimal places. - Equilateral 82576
 Calculate the volume and surface area of a 9.6 cm high prism with a base of an equilateral triangle of length 4.8 cm.
Calculate the volume and surface area of a 9.6 cm high prism with a base of an equilateral triangle of length 4.8 cm. - Substantial 65114
 Calculate the volume of a regular triangular prism with a substantial edge length of 8 cm and a prism height of 17 cm.
Calculate the volume of a regular triangular prism with a substantial edge length of 8 cm and a prism height of 17 cm. - Surface 64744
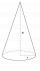 The cone is 12 cm high, and the radius of the figure is 9 cm. Find out its surface.
The cone is 12 cm high, and the radius of the figure is 9 cm. Find out its surface. - Surrounded 8283
 The cube has an edge length of 5 cm. This cube surrounds a rotating cylinder. Find the surface area of the shell and the volume of the cylinder.
The cube has an edge length of 5 cm. This cube surrounds a rotating cylinder. Find the surface area of the shell and the volume of the cylinder. - Quadrangular prism
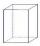 Calculate the volume and surface area of a regular quadrangular prism 35 cm high and the base diagonal 22 cm.
Calculate the volume and surface area of a regular quadrangular prism 35 cm high and the base diagonal 22 cm. - Cube wall
 The perimeter of one cube wall is 120 meters. Calculate the surface area and the body diagonal of this cube.
The perimeter of one cube wall is 120 meters. Calculate the surface area and the body diagonal of this cube. - Square base - prism
 The right prism has a square base with a side 3 cm long. The diagonal of the sidewall of the prism is u = 5cm. Calculate its volume.
The right prism has a square base with a side 3 cm long. The diagonal of the sidewall of the prism is u = 5cm. Calculate its volume. - Cone
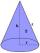 Calculate the volume of the rotating cone with a base radius of 26.3 cm and a side 38.4 cm long.
Calculate the volume of the rotating cone with a base radius of 26.3 cm and a side 38.4 cm long. - Concrete block
 Determine the volume of the concrete block whose one edge of the base is 3 meters long, the body diagonal is 13 meters, and the height is 12 meters.
Determine the volume of the concrete block whose one edge of the base is 3 meters long, the body diagonal is 13 meters, and the height is 12 meters. - Cube - angles
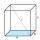 Calculate the angle alpha (α) between the wall diagonal and cube base. Calculate the angle beta (β) between the cube body diagonal and the cube base.
Calculate the angle alpha (α) between the wall diagonal and cube base. Calculate the angle beta (β) between the cube body diagonal and the cube base. - Parallelogram
 We know about parallelogram ABCD: length |AB| = 76cm, |BC| = 44cm, and angle ∢BAD = 30°. Find the area of the parallelogram.
We know about parallelogram ABCD: length |AB| = 76cm, |BC| = 44cm, and angle ∢BAD = 30°. Find the area of the parallelogram. - Trapezoid 65644
 In an isosceles trapezoid, the base ratio a / c = 9/7, arm b = 10 cm, height v = 8 cm. Calculate the area of the trapezoid in cm².
In an isosceles trapezoid, the base ratio a / c = 9/7, arm b = 10 cm, height v = 8 cm. Calculate the area of the trapezoid in cm². - Rectangular 18993
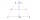 The bases are 9 cm and 50 mm long in a rectangular trapezoid. The length of the shorter arm is 3 cm. Calculate the circuit and area.
The bases are 9 cm and 50 mm long in a rectangular trapezoid. The length of the shorter arm is 3 cm. Calculate the circuit and area. - Vector
 Calculate the length of the vector v&; 8407; = (0.75, 5.5, 7.25, 1.25).
Calculate the length of the vector v&; 8407; = (0.75, 5.5, 7.25, 1.25). - Inscribed and described circle
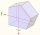 Find the radii of a circle inscribed and circumscribed by a regular pentagon whose side measures 3 cm.
Find the radii of a circle inscribed and circumscribed by a regular pentagon whose side measures 3 cm. - Decadal - flower bed
 The castle park includes a flower bed in the shape of a regular decagon with an area of 432.8 m². Determine the distance between the adjacent vertices of the flower bed.
The castle park includes a flower bed in the shape of a regular decagon with an area of 432.8 m². Determine the distance between the adjacent vertices of the flower bed. - Rhumbline
 Find the circumference and area of the rhumbline ABCD if the short side AD has a length of 5 cm, and the heel of the height from D leading to the AB side divides the AB side into two sections of 3 cm and 4 cm.
Find the circumference and area of the rhumbline ABCD if the short side AD has a length of 5 cm, and the heel of the height from D leading to the AB side divides the AB side into two sections of 3 cm and 4 cm. - Maturitný - RR - base
 In an isosceles triangle ABC with base AB, ∠BAC = 20°, AB = 4. The axis of the interior angle at vertex B intersects side AC at point P. Calculate the length of the segment AP. Give the result to two decimal places.
In an isosceles triangle ABC with base AB, ∠BAC = 20°, AB = 4. The axis of the interior angle at vertex B intersects side AC at point P. Calculate the length of the segment AP. Give the result to two decimal places. - Circumference 5487
 Calculate the solid diagonal of a cube if you know that the circumference of one of its walls equals 39 centimeters.
Calculate the solid diagonal of a cube if you know that the circumference of one of its walls equals 39 centimeters.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
