Volume - math word problems - page 43 of 126
Number of problems found: 2516
- Metal balls
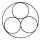Four metal balls with a diameter of 5 cm are placed in a measuring cylinder with an inner diameter of 10 cm. What is the smallest water volume to be poured into the cylinder so that all balls are below the water level? - Truncated pyramid
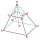The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base. - A semi-circular
A semi-circular fishbowl is filled with water and has a diameter of 10 feet. What is the total water weight to the nearest pound in the tank if water weighs 62.5 pounds per cubic foot? - Painting classrooms
Martha solicited 3 2/3 liters of paint for the brigade. Their city mayor gave their school another 2 2/5 liters of paint. How many classrooms can be painted if each classroom needs 1 3/7 liters? - The tetrahedron
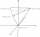Calculate a regular tetrahedron's surface area and volume 4.9 cm high, and the base edge has a length of 6 cm. - Deceleration
In a braking test, a vehicle that travels at 51 km/h stops in 5 s. What is its acceleration? - Pyramidal 44061
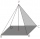A pyramidal candle with a square base has a side edge of s = 12 cm and a base edge of 4 cm. How much wax will we need to make it, and how long is the wick if it is 5% bigger than its height? - Liters 44041
What is the length of the edge of a cube with a volume of V = 1728 liters? - Liters 44031
What is the width of a block with volume V = 600 liters if a = 120cm, b = 50cm? - Petra
Petra likes to bathe in a bathtub with a water temperature of 38 degrees. She turned on the hot water set at 70 degrees and left for a moment. Before she returned, 40 liters of water flowed into the tub. How much water with a temperature of 22 degrees mus - The block
The block, the edges formed by three consecutive GP members, has a surface area of 112 cm². The sum of the edges that pass through one vertex is 14 cm. Calculate the volume of this block. - Consider
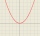Consider all square prisms with a height of 10 cm. If x is the measurement of the base edge in cm, and y is the prism's volume in cm³. Graph the function - Calculate 43951
Calculate the radius of the base of the cylinder with a volume of 10 dm³ and a height of 15 cm. - Truncated 43851
The pit is a regular truncated 4-sided pyramid, with 14 m and 10 m base edges and a depth of 6m. Calculate how much m³ of soil was removed when we dug this pit. - Reservoir - water tank
The reservoir has the shape of a sphere with a diameter of 14 m. a) How many hectoliters (hl) of water can it hold? b) How many kg of paint is needed to paint the reservoir if it is painted three times and one kg of paint is enough to paint about 9 m²? - Gallons and quarts
5 gallons 2 quarts − 1 gallon 3 quarts = (Hint: 4 quarts equals 1 gallon. ) - Transported 43451
A sandpit on a playground is shaped like a circle with a diameter of 3 meters and a depth of 25cm. How many cubic meters of sand are needed? Determine the weight of the transported sand if 1 m³ of sand weighs 800 kg. - The square
The square oak board (with density ρ = 700 kg/m3) has a side length of 50 cm and a thickness of 30 mm. 4 holes with a diameter of 40 mm are drilled into the board. What is the weight of the board? - Specified 43301
The water tank has the shape of a block. The bottom of the tank is square, with a side length of 3 m. There are 22,500 liters of water in the tank. To what height in meters does the water in the tank reach the specified amount? - Cone-shaped 43291 Calculate the volume and weight of a pile of cone-shaped sand with a diameter of 8m and a height of v = 4.5m; the density of sand is 1500kg/M cubic.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
