Kvadratická rovnice kalkulačka
Kvadratická rovnice má základní tvar: ax2+bx+c=0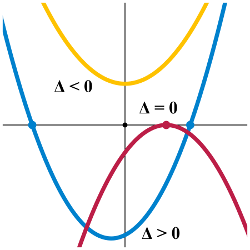
Výpočet:
12=1/2∗0,5x∗(x+2) −0,25x2−0,5x+12=0 0,25x2+0,5x−12=0 a=0,25;b=0,5;c=−12 D=b2−4ac=0,52−4⋅0,25⋅(−12)=12,25 D>0 x1,2=2a−b±D=0,5−0,5±12,25=−1±49 x1,2=−1±7 x1=6 x2=−8 Soucinovy tvar rovnice: 0,25(x−6)(x+8)=0
Textové řešení:
-0.25x2-0.5x+12=0 ... kvadratická rovniceDiskriminant:
D = b2 - 4ac = 12.25
D > 0 ... Rovnice má dva různé reálné kořeny
x1 = 6
x2 = -8
P = {6; -8}
