Boolova algebra - příklady
Pokyny: Vyřešte každý úkol pečlivě a ukažte své celé řešení. Pokud je to vhodné, proveďte zkoušku správnosti řešení.Počet nalezených příkladů: 60
- Dopravních 84293
Z celkového počtu dopravních nehod se 80% stane v obci a 20% mimo obec. Kdyby se podařilo snížit počet dopravních nehod v obci o 40%, o kolik procent by klesl celkový počet dopravních nehod? - Zaměstnanců 82035
V době krádeže bylo v hotelu 96 lidí, 61 z nich je mimo podezření. Ze 47 zaměstnanců, kteří byli v hotelu, je 23 mimo podezření. Kolik hostů není mimo podezření? - Hodíme 4
Hodíme třikrát kostkou. Vypočítejte pravděpodobnost, že při prvním, nebo druhém, nebo třetím hodu padne sudé číslo. - Pravděpodobnost 80785
Hodíme kostkou, a pak hodíme tolikrát mincí, jaké číslo padlo na kostce. Jaká je pravděpodobnost, že padne na minci alespoň jednou hlava?
- Pravděpodobnost 75174
Kapsa obsahuje 18 míčků, které se liší pouze barvou, 11 modrých a sedm červených. Pokud se vyberou dva míčky, jeden po druhém bez výměny, najděte pravděpodobnost, že oba jsou (i) Modrá (ii) stejné barvy (iii) různých barev - Pravděpodobnost 73774
Odhaduje se, že 10 % všech federálních vězňů má o sobě pozitivní obraz, 40 % má neutrální sebeobraz, zatímco zbytek má o sobě negativní obraz. Odhadovaná pravděpodobnost rehabilitace vězně s negativním sebeobrazem je 0,1. U neutrálního sebeobrazu je tato - Pravděpodobnosti 73014
Na jisté vysoké škole je účetnictví jedním z kurzů; mezi studenty účetnictví je 60% mužů. Mezi studenty uspělo 75 % a mezi ženami 50 % neuspělo. a) prezentujte to pomocí diagramu stromu pravděpodobnosti b) určit pravděpodobnost, že náhodně vybraný student - Určete 39
Určete pravděpodobnost, že při třech hodech kostkou padne aspoň jednou 1. - Neekvivalence
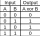Napiš funkci logická neshoda – výlučný součet (neekvivalence) F = A ⊕ B (EXL –OR) jiným zápisem a nakresli karnaughovu mapu. Pomocí prvků NAND realizuj uvedenou funkci máš-li k dispozici pouze proměnné A a B
- Jaká je 4
Jaká je pravděpodobnost, že libovolné dvojciferné číslo a) je dělitelné pěti, b) není dělitelné pěti? - Terč je 2
Terč je rozdělen na tři pásma. Pravděpodobnost, že střelec zasáhne první pásmo, je 0,18, druhé pásmo 0,2, třetí pásmo 0,44. Jaká je pravděpodobnost, že a) zasáhne terč, b) mine cíl? - Pravděpodobné 66014
Viktorie má spoustu triček - 3 bílé, 1 žluté, 3 modré, 2 zelené, 4 růžové, 1 černé, 2 oranžové. Které z následujících tvrzení je pravdivé? A: Je stejně pravděpodobné, že si Viktorie oblékne bílé jako růžové tričko. B: Je více pravděpodobné, že si Viktorie - Knihkupectví 64284
Knihkupectví Levný Jožko snižuje ceny knih o matematice k propagaci. Obchod má 6 knih o algebře, 6 knih o geometrii a 5 knih o statistice, které lze uspořádat na polici. Knihy stejného druhu se umístí vedle sebe. Kolika způsoby mohou být tyto knihy uspořá - Pravděpodobnost 63164 V zemi pije kávu 65 % lidí, 50 % pije čaj a 25 % pije obojí. Jaká je pravděpodobnost, že náhodně vybraná osoba nebude pít ani čaj ani kávu?
- Sázíme
Sázíme 2 druhy růží (bílé a červené). Ze zkušenosti vyplývá, že pravděpodobnost vyklíčení červené růže je 0,7. Celkem je vysazeno 5 sazenic. Jaká je pravděpodobnost, že: a) první 2 budou červené a další bílé b) všechny budou červené c) ani jedna nebude če - Španělštinu 59633
Účastníci kongresu mohou své příspěvky přednést v angličtině, italštině nebo španělštině. Každý ze 120 účastníků ovládá alespoň dva tyto jazyky a 10 účastníků hovoří všemi třemi jazyky. Anglicky a španělsky mluví právě tolik účastníků, kolik ovládá anglič - Stanovte
Stanovte pravděpodobnost náhodného jevu, že z 10 náhodně vybraných bridžových karet budou alespoň 3 esa. Pozn. jedná se o týmovou hru, přičemž v balíčku je 52 karet, z toho 4 esa. - Následujících 58241
Jestliže P je množina násobků 2, Q je množina násobků 3 a R je množina násobků 7, které z následujících celých čísel bude v P a Q, ale ne v R? A = -54 B = -50 C=42 D=100 E=252 - Prázdniny
Děti se ve škole bavily o tom, jak strávily prázdniny. Na dovolené s rodiči byly 2/3 z nich. U moře bylo 10 dětí, což je 5/8 z těch, které byly na dovolené. Kolik je ve třídě dětí?
V dílně se k výrobě židlí používají tři roboty Q, R a S Robot Q tvoří 25% židlí Robot R tvoří 45% židlí Zbývající židle vyrobil Robot S Důkazy ukázaly, že 2 procenta židlí vyrobených robotem Q jsou vadné, 3 procenta židlí vyrobených robotem R a 5 procent Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
