Účastníci kongresu
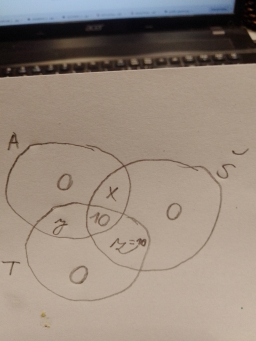
Účastníci kongresu mohou své příspěvky přednést v angličtině, italštině nebo španělštině. Každý ze 120 účastníků ovládá alespoň dva tyto jazyky a 10 účastníků hovoří všemi třemi jazyky. Anglicky a španělsky mluví právě tolik účastníků, kolik ovládá angličtinu a italštinu, ale neumí španělsky. Španělštinu a italštinu, ale bez angličtiny ovládá stejný počet účastníků, jako je ty, kteří mluví všemi třemi jazyky.
Určete pomocí Vennova diagramu:
Angličtinu ovládá a účastníky.
Angličtinu neovládá A účastníky.
Španělštinu ovládá s účastníky.
Španělštinu neovládá S účastníků.
Italštinu ovládá t účastníků.
Italštinu neovládá T účastníků.
Angličtinu a italštinu ovládá q účastníků.
Angličtinu a španělštinu ovládá w účastníky.
Italštinu a španělštinu ovládá e účastníky.
Vaše odpověď:
Určete pomocí Vennova diagramu:
Angličtinu ovládá a účastníky.
Angličtinu neovládá A účastníky.
Španělštinu ovládá s účastníky.
Španělštinu neovládá S účastníků.
Italštinu ovládá t účastníků.
Italštinu neovládá T účastníků.
Angličtinu a italštinu ovládá q účastníků.
Angličtinu a španělštinu ovládá w účastníky.
Italštinu a španělštinu ovládá e účastníky.
Vaše odpověď:
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebrazákladní operace a pojmytémaÚroveň náročnosti úkolu
Související a podobné příklady:
- Studenti a jazyky
Každý z 30 studentů každý ovládá angličtinu nebo němčinu. Tři z nich ovládají oba jazyky. Ty, kteří mluví pouze německy, je o třech více než ty, kteří mluví pouze anglicky. Vypočítejte pomocí vennova diagramu: Angličtinu ovládá a studenty. Pouze anglicky - Světové jazyky
Ve třídě je 50 žáků. Z tohoto počtu 1/10 hovoří pouze francouzsky a 4/5 z deseti hovoří francouzsky i anglicky. Pokud zbytek mluví pouze anglicky, najděte počet žáků, kteří mluví pouze anglicky. - Jazyky na recepci
Na recepci na velvyslanectví každý ovládá alespoň jeden cizí jazyk: 15 lidí mluví anglicky 12 lidí mluví německy 7 oběma Z kolika lidí se skládá tato společnost, pokud v ní nikdo nemluví jiným jazykem? - Cizí jazyk
Studenti VŠ si při zápisu vybírali cizí jazyk do 1. ročníku. Mezi 120 zapsaných studentů si 75 zvolilo angličtinu, 65 němčinu a 40 i angličtinu a také němčinu. Použitím Vennovho diagramu určete: - kolik ze zapsaných studentů si zvolilo pouze angličtinu - - Účastníci soutěže
V matematické soutěži řešili její účastníci dva úkoly. Každý vyřešil alespoň jednu úlohu, přitom první úlohu vyřešilo 80 % účastníků, druhou úlohu 50 %. Obě úkoly vyřešilo 60 účastníků. Kolik účastníků měla soutěž? - Soutěž
V soutěži bylo možné získat 0 až 5 bodu. Ve skutečnosti každý z 15 nejlepších soutěžících získal 5 bodu (které získali 5 soutěžících), nebo 4 body (které získali 10 soutěžících). Počet soutěžících, kteří získali 3 body, byl stejný jako počet soutěžících, - Štafetové týmy
Je 159 studentů, kteří se mají rozdělit do štafetových týmů. Každý tým by měl mít stejný počet studentů. Může mít každý tým 3, 5 nebo 6 studentů? Vysvětlete.
