Množiny - příklady - strana 5 z 12
Počet nalezených příkladů: 227
- Neprázdné 34291
 Pro dvě neprázdné množiny A, B platí: A ∪ B má 16 prvků, A ∩ B má 11 prvků a množina A – B je prázdná. Kolik prvků má množina B-A?
Pro dvě neprázdné množiny A, B platí: A ∪ B má 16 prvků, A ∩ B má 11 prvků a množina A – B je prázdná. Kolik prvků má množina B-A? - Cizí jazyk
 Studenti VŠ si při zápisu vybírali cizí jazyk do 1. ročníku. Mezi 120 zapsaných studentů si 75 zvolilo angličtinu, 65 němčinu a 40 i angličtinu a také němčinu. Použitím Vennovho diagramu určete: - kolik ze zapsaných studentů si zvolilo pouze angličtinu -
Studenti VŠ si při zápisu vybírali cizí jazyk do 1. ročníku. Mezi 120 zapsaných studentů si 75 zvolilo angličtinu, 65 němčinu a 40 i angličtinu a také němčinu. Použitím Vennovho diagramu určete: - kolik ze zapsaných studentů si zvolilo pouze angličtinu - - Kurz angličtiny
 Ze 60 zaměstnanců firmy 28 chodí na kurz angličtiny, 17 na kurz němčiny a 20 lidí nechodí na žádný z těchto kurzů. Kolik zaměstnanců chodí na oba uvedené kurzy?
Ze 60 zaměstnanců firmy 28 chodí na kurz angličtiny, 17 na kurz němčiny a 20 lidí nechodí na žádný z těchto kurzů. Kolik zaměstnanců chodí na oba uvedené kurzy? - Prosím 5
 Prosím, stanov podmínky řešitelnosti rovnice, vyřeš rovnici a proveď zkoušku, x lomeno x na druhou mínus 2x plus1 to celé mínus x+3 lomeno x na druhou mínus 1 to celé rovná se 0 x/(x²-2x+1) - (x+3)/( x²-1) = 0
Prosím, stanov podmínky řešitelnosti rovnice, vyřeš rovnici a proveď zkoušku, x lomeno x na druhou mínus 2x plus1 to celé mínus x+3 lomeno x na druhou mínus 1 to celé rovná se 0 x/(x²-2x+1) - (x+3)/( x²-1) = 0 - Kvadratickou 33371
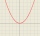 Řešte kvadratickou nerovnici: -2x² + 4x + 6 < 0
Řešte kvadratickou nerovnici: -2x² + 4x + 6 < 0 - Nedostatky
 Při hygienické kontrole v 2000 zařízeních společného stravování byly nedostatky zjištěny v 300 zařízeních. Jaká je pravděpodobnost, že při kontrole 10 zařízení budou zjištěny nedostatky v nejvíce 3 zařízeních?
Při hygienické kontrole v 2000 zařízeních společného stravování byly nedostatky zjištěny v 300 zařízeních. Jaká je pravděpodobnost, že při kontrole 10 zařízení budou zjištěny nedostatky v nejvíce 3 zařízeních? - Dvouciferné 26211
 Pomocí číslic 4 a 7 napíše všechny dvouciferné čísla
Pomocí číslic 4 a 7 napíše všechny dvouciferné čísla - Pravděpodobnost 25351
 V dávce 500 výrobků je 10 zmetků. Při statistické prověrce se kontroluje 40 výrobků, které jsou náhodně vybrány z dávky, přičemž se provádí výběr bez opakování. Dávka je posouzena jako vyhovující, pokud mezi 40 kontrolovanými výrobky je nejvýše jeden zmet
V dávce 500 výrobků je 10 zmetků. Při statistické prověrce se kontroluje 40 výrobků, které jsou náhodně vybrány z dávky, přičemž se provádí výběr bez opakování. Dávka je posouzena jako vyhovující, pokud mezi 40 kontrolovanými výrobky je nejvýše jeden zmet - Pravděpodobnost 25181
 Statisticky se zjistilo, že ve městě se 100 000 obyvateli během jednoho roku zemře 600 lidí. Do nemocničního léčení se během roku dostane 2000 lidí a z nich tam zemře 120 osob. Vypočítejte pravděpodobnost, že občan, který se přijde léčit do nemocnice, zem
Statisticky se zjistilo, že ve městě se 100 000 obyvateli během jednoho roku zemře 600 lidí. Do nemocničního léčení se během roku dostane 2000 lidí a z nich tam zemře 120 osob. Vypočítejte pravděpodobnost, že občan, který se přijde léčit do nemocnice, zem - Označeni 22133
 Ve škole bylo 40 chlapců. Byli označeni čepicemi a tričky. 25 chlapců mělo modrou čepici. 20 chlapců mělo modrou čepici a žluté tričko. a) Kolik chlapců mělo žluté triko? b) Kolik chlapců nemělo modrou čepici? c) Kolik chlapců mělo jen žluté triko?
Ve škole bylo 40 chlapců. Byli označeni čepicemi a tričky. 25 chlapců mělo modrou čepici. 20 chlapců mělo modrou čepici a žluté tričko. a) Kolik chlapců mělo žluté triko? b) Kolik chlapců nemělo modrou čepici? c) Kolik chlapců mělo jen žluté triko? - Double pravděpodobnost
 Pravděpodobnost úspěchu plánované akce je 60%. Jaká je pravděpodobnost, že při dvojnásobném opakování této akce se alespoň jednou dosáhne úspěch?
Pravděpodobnost úspěchu plánované akce je 60%. Jaká je pravděpodobnost, že při dvojnásobném opakování této akce se alespoň jednou dosáhne úspěch? - V zahrádce
 V zahrádce bylo 35 květů. Motyle byly na 17 květech. Na 8 květech byly motýly i včely. Vést zjistit na kolika květech byly jen včely? Pozn. na každém květu byl maximálně jeden motýl a maximálně jedna včela. Každý květ byl obsazen.
V zahrádce bylo 35 květů. Motyle byly na 17 květech. Na 8 květech byly motýly i včely. Vést zjistit na kolika květech byly jen včely? Pozn. na každém květu byl maximálně jeden motýl a maximálně jedna včela. Každý květ byl obsazen. - Součet nebo stejné
 Určete pravdepodobnost, že při hodu 2 kostkami padne součet 10 nebo stejné číslo na obou kostkách.
Určete pravdepodobnost, že při hodu 2 kostkami padne součet 10 nebo stejné číslo na obou kostkách. - Na univerzitě
 Na určité univerzitě je 25% studentů obchodní fakulty. Ze studentů obchodní fakulty je 66% mužů. Avšak pouze 52% všech studentů na univerzitě jsou muži. a. Jaká je pravděpodobnost, že náhodně vybraný student na univerzitě je muž na obchodní fakultě? b. Ja
Na určité univerzitě je 25% studentů obchodní fakulty. Ze studentů obchodní fakulty je 66% mužů. Avšak pouze 52% všech studentů na univerzitě jsou muži. a. Jaká je pravděpodobnost, že náhodně vybraný student na univerzitě je muž na obchodní fakultě? b. Ja - Sledování 15793
 Počet hodin sledování televize denně na vzorku 28 lidí je uveden níže: 4, 1, 5, 5, 2, 5, 4, 4, 2, 3, 6, 8, 3, 5, 2, 0, 3, 5, 9, 4, 5, 2, 1, 3, 4, 7, 2, 9 Jaká je střední hodnota?
Počet hodin sledování televize denně na vzorku 28 lidí je uveden níže: 4, 1, 5, 5, 2, 5, 4, 4, 2, 3, 6, 8, 3, 5, 2, 0, 3, 5, 9, 4, 5, 2, 1, 3, 4, 7, 2, 9 Jaká je střední hodnota? - Trojuholník 333
 V rovině jsou dány body A, B a C vzdálené od sebe 3 cm, přičemž neleží v jedné přímce. Vyznač množinu všech bodů, jejichž vzdálenost je od všech tří bodů menší nebo rovna 2,5 cm.
V rovině jsou dány body A, B a C vzdálené od sebe 3 cm, přičemž neleží v jedné přímce. Vyznač množinu všech bodů, jejichž vzdálenost je od všech tří bodů menší nebo rovna 2,5 cm. - 73 studentů
 Prosím o vypočítání tohoto příkladu podle vennových rovnic: Ptali se 73 studentů, zda mají rádi vánoce či velikonoce. 34 z nich má rádo jeden ze svátků. 39 má rádo velikonoce a dvakrát tolik je studentů, kteří mají rádi oba svátky, než je těch, kteří mají
Prosím o vypočítání tohoto příkladu podle vennových rovnic: Ptali se 73 studentů, zda mají rádi vánoce či velikonoce. 34 z nich má rádo jeden ze svátků. 39 má rádo velikonoce a dvakrát tolik je studentů, kteří mají rádi oba svátky, než je těch, kteří mají - Narýsuj 4
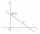 Narýsuj do jednoho obrazku : a) přímku RZ b) YZ, pro kterou platí YZ je kolmá k RZ c) polopřímku RS různoběžnou s YZ i s přímkou RZ d) bod F, který leží na YZ mimo již zvolené body e) bod H, který leží na polopřímce RS i přímce RZ
Narýsuj do jednoho obrazku : a) přímku RZ b) YZ, pro kterou platí YZ je kolmá k RZ c) polopřímku RS různoběžnou s YZ i s přímkou RZ d) bod F, který leží na YZ mimo již zvolené body e) bod H, který leží na polopřímce RS i přímce RZ - Dvě množiny
 Předpokládejme, že množina B obsahuje 69 prvků a celkový počet prvků v množině A nebo množině B je 124. Pokud množiny A a B mají společných 29 prvků, kolik prvků je obsažených v množině A?
Předpokládejme, že množina B obsahuje 69 prvků a celkový počet prvků v množině A nebo množině B je 124. Pokud množiny A a B mají společných 29 prvků, kolik prvků je obsažených v množině A? - Zaměstnanců 12961
 Polovinu zaměstnanců tvoří ženy. 2/5 jsou matky. Jakou část zaměstnanců tvoří matky?
Polovinu zaměstnanců tvoří ženy. 2/5 jsou matky. Jakou část zaměstnanců tvoří matky?
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
