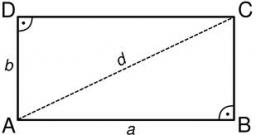
Rectangle SS
The perimeter of a rectangle is 154 dm and its diagonal is 62.36 dm. Find the dimensions of the rectangle.
Final Answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetrynumbersUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Perimeter and diagonal
The perimeter of the rectangle is 82 m, and the length of its diagonal is 29 m. Find the dimensions of the rectangle. - Rectangular plot
The dimensions of a rectangular plot are (x + 1) m and (2x − y) m. The sum of x and y is 3 m and the perimeter of the plot is 36 m. Find the area of the plot and the length of its diagonal. - Cuboid
Find the dimensions a, b, and c of a cuboid whose space diagonal is d = 6 dm and makes an angle α = 35° with edge a and an angle β = 66° with edge b. - Rectangle perimeter
The width of the rectangle is 65% of the length. Calculate the lengths of the sides of a rectangle if its perimeter is 132 dm. - Rectangular field
A rectangular field has a diagonal length of 169 m. If the length and width are in the ratio of 12:5. Find the field's dimensions, the field's perimeter, and the field's area. - Diagonal
Determine the dimensions of a cuboid whose space diagonal is 60 dm and makes an angle of 35° with one edge and 77° with another edge. - Rectangle
The width of the rectangle is 65% of its length, and its perimeter is 132 cm. Determine the dimensions of the rectangle.
