Building
How high is the building that throws horizontal shadow 85.6 m long at angle 34°12'?
Correct answer:

Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Reflector
 The circular reflector throws a light cone with a vertex angle 49° and is on 33 m height tower. The axis of the light beam has the axis of the tower angle 30°. What is the maximum length of the illuminated horizontal plane?
The circular reflector throws a light cone with a vertex angle 49° and is on 33 m height tower. The axis of the light beam has the axis of the tower angle 30°. What is the maximum length of the illuminated horizontal plane? - Sun rays
 If the sun's rays are at an angle of 60°, then the famous Great Pyramid of Egypt (which is now 137.3 meters high) has a 79.3 m long shadow. Calculate the current height of the neighboring Chephren pyramid, whose shadow is measured at the same time at 78.8
If the sun's rays are at an angle of 60°, then the famous Great Pyramid of Egypt (which is now 137.3 meters high) has a 79.3 m long shadow. Calculate the current height of the neighboring Chephren pyramid, whose shadow is measured at the same time at 78.8 - The shadow
 The shadow of a 1 m high pole thrown on a horizontal plane is 0.8 m long. At the same time, the shadow of a tree thrown on a horizontal plane is 6.4 m. Determine the height of the tree.
The shadow of a 1 m high pole thrown on a horizontal plane is 0.8 m long. At the same time, the shadow of a tree thrown on a horizontal plane is 6.4 m. Determine the height of the tree. - Shadow
 A meter pole perpendicular to the ground throws a shadow of 40 cm long. The house throws a shadow 6 meters long. What is the height of the house?
A meter pole perpendicular to the ground throws a shadow of 40 cm long. The house throws a shadow 6 meters long. What is the height of the house?
- Tree shadow
 The tree perpendicular to the horizontal surface has a shadow 8.32 meters long. At the same time, a one-meter rod perpendicular to the horizontal surface has a shadow 64 cm long. How tall is the tree?
The tree perpendicular to the horizontal surface has a shadow 8.32 meters long. At the same time, a one-meter rod perpendicular to the horizontal surface has a shadow 64 cm long. How tall is the tree? - Mast shadow
 The mast has a 13 m long shadow on a slope rising from the mast foot in the direction of the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines.
The mast has a 13 m long shadow on a slope rising from the mast foot in the direction of the shadow angle at an angle of 15°. Determine the height of the mast if the sun above the horizon is at an angle of 33°. Use the law of sines. - Horizontal 64864
 The meter stick is located on the meridian plane and deviated from the horizontal plane to the north by an angle of magnitude 70°. Calculate the length of the shadow cast by a meter stick at true noon if the Sun culminates at an angle of 41°03'.
The meter stick is located on the meridian plane and deviated from the horizontal plane to the north by an angle of magnitude 70°. Calculate the length of the shadow cast by a meter stick at true noon if the Sun culminates at an angle of 41°03'. - A radio antenna
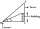 Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - Determine 82470
 The school building casts a shadow 16 m long on the plane of the yard, and at the same time, a vertical meter pole casts a shadow 132 cm long. Determine the height of the building.
The school building casts a shadow 16 m long on the plane of the yard, and at the same time, a vertical meter pole casts a shadow 132 cm long. Determine the height of the building.
- Building elevation angle
 In the building, I focused at an angle 30°. When I moved the 5 m building, I focused at an angle 45°. What is the height of the building?
In the building, I focused at an angle 30°. When I moved the 5 m building, I focused at an angle 45°. What is the height of the building? - Mast
 Mast has 13 m long shadow on a slope rising from the mast foot in the direction of the shadow angle at angle 13.3°. Determine the height of the mast if the sun above the horizon is at an angle 45°12'.
Mast has 13 m long shadow on a slope rising from the mast foot in the direction of the shadow angle at angle 13.3°. Determine the height of the mast if the sun above the horizon is at an angle 45°12'. - Building 67654
 The 15 m high building is 30 m away from the river bank. The river's width can be seen from the roof of this building at an angle of 15 °. How wide is the river?
The 15 m high building is 30 m away from the river bank. The river's width can be seen from the roof of this building at an angle of 15 °. How wide is the river? - Vertical 29801
 The shadow of the building is 16 m long, and the shadow of the vertical meter rod is 0.8 m long at the same time. What is the height of the building?
The shadow of the building is 16 m long, and the shadow of the vertical meter rod is 0.8 m long at the same time. What is the height of the building? - Similarity 26441
 How long a shadow casts a building 15 m high if the shadow of a meter rod is 90 cm? Sketch - similarity.
How long a shadow casts a building 15 m high if the shadow of a meter rod is 90 cm? Sketch - similarity.
- One side
 One side is 36 long with a 15° incline. What is the height at the end of that side?
One side is 36 long with a 15° incline. What is the height at the end of that side? - Water 71
 Water was heated to 80°c then allowed to cool at a rate of 6°c per minute. After how long was the temperature 8°C?
Water was heated to 80°c then allowed to cool at a rate of 6°c per minute. After how long was the temperature 8°C? - Observation 82708
 At the top of the hill, there is a 30-meter-high observation tower. We can see its heel and shelter from a certain point in the valley at elevation angles a=28°30" and b=30°40". How high is the top of the hill above the horizontal plane of the observation
At the top of the hill, there is a 30-meter-high observation tower. We can see its heel and shelter from a certain point in the valley at elevation angles a=28°30" and b=30°40". How high is the top of the hill above the horizontal plane of the observation
