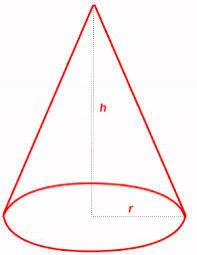
Rotary cone
The volume of the rotation of the cone is 472 cm3. The angle between the side of the cone and the base angle is 70°. Calculate the lateral surface area of this cone.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- arithmetic
- cube root
- solid geometry
- cone
- surface area
- planimetrics
- right triangle
- triangle
- goniometry and trigonometry
- cosine
- tangent
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Cut and cone
 Calculate the volume of the rotation cone whose lateral surface is a circular arc with radius 15 cm and central angle 63 degrees.
Calculate the volume of the rotation cone whose lateral surface is a circular arc with radius 15 cm and central angle 63 degrees. - Cone
 Calculate the volume and surface area of the cone with a diameter of the base d=15 cm and the side of the cone with the base has angle 52°.
Calculate the volume and surface area of the cone with a diameter of the base d=15 cm and the side of the cone with the base has angle 52°. - Pyramid 8
 Calculate the volume and the surface area of a regular quadrangular pyramid with a base side of 9 cm and a side wall with the base has an angle of 75°.
Calculate the volume and the surface area of a regular quadrangular pyramid with a base side of 9 cm and a side wall with the base has an angle of 75°. - Lateral surface area
 The ratio of the area of the base of the rotary cone to its lateral surface area is 3:5. Calculate the surface and volume of the cone if its height v = 4 cm.
The ratio of the area of the base of the rotary cone to its lateral surface area is 3:5. Calculate the surface and volume of the cone if its height v = 4 cm.
- The cone
 The cone's lateral surface area is 4 cm², and the area of the base is 2 cm². Find the angle in degrees (deviation) of the cone sine and the cone base plane. (Cone side is the segment joining the vertex cone with any point of the base circle. All sides of
The cone's lateral surface area is 4 cm², and the area of the base is 2 cm². Find the angle in degrees (deviation) of the cone sine and the cone base plane. (Cone side is the segment joining the vertex cone with any point of the base circle. All sides of - Calculate 3019
 The height is 5 cm, and the size of the angle that the side of the cone with the base makes is 63 degrees. Calculate the surface and volume of this cone.
The height is 5 cm, and the size of the angle that the side of the cone with the base makes is 63 degrees. Calculate the surface and volume of this cone. - Deviation 70744
 Calculate the volume and surface of the rotating cone if its height is 10 cm and the side has a deviation of 30 ° from the base plane.
Calculate the volume and surface of the rotating cone if its height is 10 cm and the side has a deviation of 30 ° from the base plane. - Conical area
 A right-angled triangle has sides a=12 and b=19 at the right angle. The hypotenuse is c. If the triangle rotates on the c side as an axis, find the volume and surface area of the conical area created by this rotation.
A right-angled triangle has sides a=12 and b=19 at the right angle. The hypotenuse is c. If the triangle rotates on the c side as an axis, find the volume and surface area of the conical area created by this rotation. - Side edges
 The regular 4-sided pyramid has a body height of 2 dm, and the opposite side edges form an angle of 70°. Calculate the surface area and volume of the pyramid.
The regular 4-sided pyramid has a body height of 2 dm, and the opposite side edges form an angle of 70°. Calculate the surface area and volume of the pyramid.
- Determine 82032
 Determine the volume and surface area of a cone whose slope of length 8 cm makes an angle of 75 degrees with the plane of the base.
Determine the volume and surface area of a cone whose slope of length 8 cm makes an angle of 75 degrees with the plane of the base. - The volume
 The volume of the rotating cone is 376.8cm³. The height of this cone is one dm. Calculate the diameter of the cone base.
The volume of the rotating cone is 376.8cm³. The height of this cone is one dm. Calculate the diameter of the cone base. - Calculate 82700
 A cone of rotation with a radius of 32 cm and side length s = 65 cm is given. Calculate the surface area and volume.
A cone of rotation with a radius of 32 cm and side length s = 65 cm is given. Calculate the surface area and volume. - Right-angled trapezoid
 A right-angled trapezoid with the measure of the acute angle of 50° is given. The lengths of its bases are 4 and 6 units. The volume of the solid obtained by rotation of the given trapezoid about the longer base is:
A right-angled trapezoid with the measure of the acute angle of 50° is given. The lengths of its bases are 4 and 6 units. The volume of the solid obtained by rotation of the given trapezoid about the longer base is: - Volume of the cone
 Calculate the cone's volume if its base area is 78.5 cm² and the shell area is 219.8 cm².
Calculate the cone's volume if its base area is 78.5 cm² and the shell area is 219.8 cm².
- The farmer field
 The field has a parallelogram shape with dimensions side a = 75 m and height 372 m. Two and two sides are at an angle 75°. Calculate the acreage of the field in hectares.
The field has a parallelogram shape with dimensions side a = 75 m and height 372 m. Two and two sides are at an angle 75°. Calculate the acreage of the field in hectares. - Calculate 82690
 A cone of rotation with a height of 18 cm and side length s = 45 cm is given. Calculate the surface area and volume.
A cone of rotation with a height of 18 cm and side length s = 45 cm is given. Calculate the surface area and volume. - Sphere
 Intersect between the plane and a sphere is a circle with a radius of 60 mm. The cone, whose base is this circle and whose apex is at the center of the sphere, has a height of 34 mm. Calculate the surface area and volume of a sphere.
Intersect between the plane and a sphere is a circle with a radius of 60 mm. The cone, whose base is this circle and whose apex is at the center of the sphere, has a height of 34 mm. Calculate the surface area and volume of a sphere.
