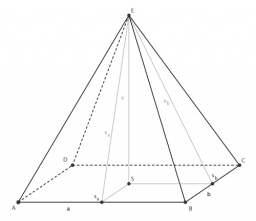
The quadrilateral pyramid
The quadrilateral pyramid has a rectangular base of 24 cm x 3.2dm and a body height of 0.4m. Calculate its volume and surface area.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Do you want to convert length units?
Do you know the volume and unit volume, and want to convert volume units?
See also our trigonometric triangle calculator.
Do you want to convert length units?
Do you know the volume and unit volume, and want to convert volume units?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Nautical vs statue mile
 A nautical mile is the unit of length used in sea and air navigation. A nautical mile is equal to 6,076 feet. What percent of a statue mile (5,280 ft) is a nautical mile?
A nautical mile is the unit of length used in sea and air navigation. A nautical mile is equal to 6,076 feet. What percent of a statue mile (5,280 ft) is a nautical mile? - The playhouse
 The drawings of the playhouse are made on a scale of 1:50. In the drawing, the length of the cottage is 4.5 cm. How long is the playhouse actually?
The drawings of the playhouse are made on a scale of 1:50. In the drawing, the length of the cottage is 4.5 cm. How long is the playhouse actually? - ABCD on a map
 Dinesh went from place A to place B and from there to place C. A is 7.5 km from B, and B is 12.7 km from C. Ayub went from place A to place D and from there to place C. D is 9.3 km from A, and C is 11.8 km from D. Who traveled more, and by how much?
Dinesh went from place A to place B and from there to place C. A is 7.5 km from B, and B is 12.7 km from C. Ayub went from place A to place D and from there to place C. D is 9.3 km from A, and C is 11.8 km from D. Who traveled more, and by how much? - Mr. Lee
 Mr. Lee has a rope. The total length of the rope is 5 meters. He cuts off 350 centimeters of rope to use in his garden and another 75 centimeters to hang a bird feeder. What is the length of the rope he has left in centimeters?
Mr. Lee has a rope. The total length of the rope is 5 meters. He cuts off 350 centimeters of rope to use in his garden and another 75 centimeters to hang a bird feeder. What is the length of the rope he has left in centimeters?
- Saw a board
 A board of 16 3-fourths inches is cut from a board that is 3 feet long. If the width of the saw cut is one-eighth inch, what is the length of the remaining piece?
A board of 16 3-fourths inches is cut from a board that is 3 feet long. If the width of the saw cut is one-eighth inch, what is the length of the remaining piece? - A triangular
 A triangular frame has sides that measure 15’-7",20’-4", and 26’-2". What is the total length of the three sides?
A triangular frame has sides that measure 15’-7",20’-4", and 26’-2". What is the total length of the three sides? - A road
 A road on a map measures 8cm long. The scale of the map is 25000. Calculate the actual length of the road
A road on a map measures 8cm long. The scale of the map is 25000. Calculate the actual length of the road - Complete 16
 Complete the conversions below, show calculations and answers 1) 3.5 kg to gram 2) 4567ml to litres 3) R45.78 to cent 4) 5.60m to centimeters
Complete the conversions below, show calculations and answers 1) 3.5 kg to gram 2) 4567ml to litres 3) R45.78 to cent 4) 5.60m to centimeters - Sand castles
 Hana's sand castle measures 19 feet by 15 feet and has a perimeter of 68. Thomas's sand castle measures 8 yards by 6 yards. What is the difference between the two perimeters?
Hana's sand castle measures 19 feet by 15 feet and has a perimeter of 68. Thomas's sand castle measures 8 yards by 6 yards. What is the difference between the two perimeters?
- A ship 2
 A ship runs at 15 1/2 knots (pls convert to nautical miles per hour) for 3 1/2 hours. How far does the ship travel?
A ship runs at 15 1/2 knots (pls convert to nautical miles per hour) for 3 1/2 hours. How far does the ship travel? - A biker
 A biker traveled from city A to city B via city C with a uniform speed of 52 km/h. He then returned directly to city A with a uniform speed of 89 km/h. Find, in minutes, the total time of his whole journey to two decimal places. City distance A from B is
A biker traveled from city A to city B via city C with a uniform speed of 52 km/h. He then returned directly to city A with a uniform speed of 89 km/h. Find, in minutes, the total time of his whole journey to two decimal places. City distance A from B is - A lighthouse
 A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats?
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - Paper
 The drawing paper has dimensions 220mm and 308mm. Pupils should cut it into squares of the same size so that they are as large as possible. Determine the dimensions of the square in cm and the number of squares.
The drawing paper has dimensions 220mm and 308mm. Pupils should cut it into squares of the same size so that they are as large as possible. Determine the dimensions of the square in cm and the number of squares. - There 32
 There are 20 magazines in a pile. Each magazine is 5 mm thick. How high is the pile in meters?
There are 20 magazines in a pile. Each magazine is 5 mm thick. How high is the pile in meters?
- FRAMES
 Joe is making picture frames out of wood. The length of each frame is 10 inches, and the width is 8 inches. Each piece of wood used to make the frames is 8 feet long. How many pieces of wood will he need to make 10 picture frames? Clue: find the perimeter
Joe is making picture frames out of wood. The length of each frame is 10 inches, and the width is 8 inches. Each piece of wood used to make the frames is 8 feet long. How many pieces of wood will he need to make 10 picture frames? Clue: find the perimeter - Dimensions 81607
 On a 1:150000 scale map, what will be the dimensions of a strip of the forest whose actual length is 6 km and actual width is 900 meters?
On a 1:150000 scale map, what will be the dimensions of a strip of the forest whose actual length is 6 km and actual width is 900 meters? - Millimeters - saw
 A fine tooth of a saw has 60 teeth per 2 inches (1 inch = 2.54 cm). What is the tooth pitch in millimeters (rounded to hundredths of mm)?
A fine tooth of a saw has 60 teeth per 2 inches (1 inch = 2.54 cm). What is the tooth pitch in millimeters (rounded to hundredths of mm)?
