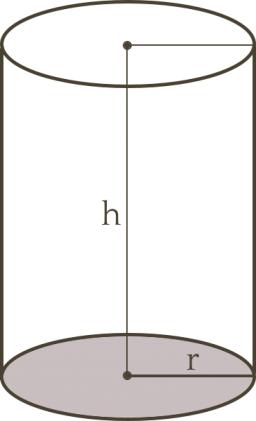
Cylinder surface, volume

The area of the cylinder surface and the cylinder jacket are in the ratio 3: 5. The height of the cylinder is 5 cm shorter than the radius of the base. Calculate surface area and volume of the cylinder.

Correct answer:

S =  10367.26 cm²
V =  70685.83 cm³

Step-by-step explanation:

$$\begin{gathered} {\displaystyle \frac{S_1}{S_2}}={\displaystyle \frac{3}{5}} \\ {\displaystyle \frac{\pi r^2}{2\pi rh}}={\displaystyle \frac{3}{5}} \\ {\displaystyle \frac{r}{2h}}={\displaystyle \frac{3}{5}} \\ 5r=6h \\ h=r-5 \\ h=25cm \\ r=30cm \\ S=2\pi r^2+2\pi rh=2\pi \cdot 30\cdot (30+25)=10367.26{\text{cm}}^2 \end{gathered}$$

$V=\pi r^{2}h=\pi 30^2\cdot 25=70685.83{\text{cm}}^3$

Try another example

Related math problems and questions:

• Axial section
  Axial section of the cylinder has a diagonal 40 cm. The size of the shell and the base surface are in the ratio 3:2. Calculate the volume and surface area of this cylinder.
• Axial section
  The axial section of the cylinder has a diagonal 31 cm long, and we know that the area of the side and the base area is in ratio 3:2. Calculate the height and radius of the cylinder base.
• Volume and surface
  Calculate the volume and surface area of the cylinder when the cylinder height and base diameter is in a ratio of 3:4 and the area of the cylinder jacket is 24 dm².
• Cylinder - basics
  Cylinder with base radius r = 54 cm and height h=35 cm. Calculate: a) Area of the base
• Lateral surface area
  The ratio of the area of the base of the rotary cone to its lateral surface area is 3: 5. Calculate the surface and volume of the cone, if its height v = 4 cm.
• Surface of the cylinder
  Calculate the surface of the cylinder for which the shell area is Spl = 20 cm² and the height v = 3.5 cm
• Curved surface area CSA
  A cylinder 5cm high has a base radius(7/2) cm. Calculate the curved surface area.
• The surface
  The surface of the cylinder is 1570 cm², its height is 15 cm. Find its volume and radius of the base.
• The volume
  The volume of a solid cylinder is 260 cm³ the cylinder is melt down into a cuboid, whose base is a square of 5cm, calculate the height of the cuboid and the surface area of the cuboid
• Equilateral cylinder
  Equilateral cylinder (height = base diameter; h = 2r) has a volume of V = 199 cm³ . Calculate the surface area of the cylinder.
• Trapezoidal base
  Calculate the surface and volume of a quadrilateral prism with a trapezoidal base, where a = 7 cm, b = 4 cm, c = 5 cm, d = 4 cm, height of trapezium v = 3.7 cm and the height of the prism h = 5 cm.
• Surface of the cylinder
  Calculate the surface area of the cylinder when its volume is 45 l and the perimeter of base is three times of the height.
• Cylinder - h
  The cylinder volume is 140 cm³. The base radius is 7 cm. Calculate the height of the cylinder.
• The diagram 2
  The diagram shows a cone with slant height 10.5cm. If the curved surface area of the cone is 115.5 cm². Calculate correct to 3 significant figures: *Base Radius *Height *Volume of the cone
• Height as diameter of base
  The rotary cylinder has a height equal to the base diameter and a surface of 471 cm². Calculate the volume of a cylinder.
• The cylinder
  In a rotating cylinder it is given: the surface of the shell (without bases) S = 96 cm² and the volume V = 192 cm cubic. Calculate the radius and height of this cylinder.
• Rotary cylinder
  In the rotary cylinder it is given: surface S = 96 cm² and volume V = 192 cm cubic. Calculate its radius and height.