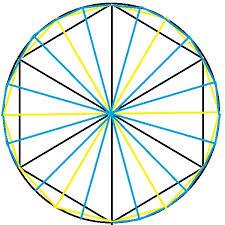
Polygon 42
Which polygon has 42 more diagonals than sides?
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Diagonals 7029
The number of diagonals of a given polygon is 88 more than the number of its sides. How many sides does this polygon have - Number of sides
Find the number of sides of a regular polygon whose each exterior angle has a measure of 45°. - Calculate deltoid
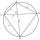Calculate the diagonals in the deltoid with sides of 10, 10, and shorter 6, 6 cm. - Diagonals
What x-gon has 54 diagonals? - Rhombus
The rhombus with area 95 has one diagonal that is longer by 7 than the second one. Calculate the length of the diagonals and rhombus sides. - Regular polygons
Two regular polygons, x and y, are such that the number of sides of x is three more than the number of the sides of y. If the sum of the exterior angles of x and y is 117°, how many sides have x? - Four sides of trapezoid
The trapezoid is given by the length of four sides: 40.5, 42.5, 52.8 35.0. Calculate its area.
