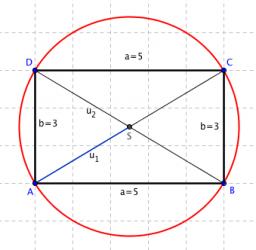
Rectangle - desc circle
The length of the sides of the rectangle is at a ratio of 1:3. The circle's radius circumscribed to the rectangle is 10 cm. Calculate the rectangle's perimeter.
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
The Pythagorean theorem is the base for the right triangle calculator.
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Circumscribed 2671
The circle's radius circumscribed by the rectangle is 5 cm, and one side of the rectangle is 6 cm long. Calculate the length of the other side and the area of the rectangle. - Rectangle - parallelogram
A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle. - Circumscription
Calculate the radius of the Circumscribed circle in the rectangle with sides 20 and 19. Can it be a rectangle inscribed by a circle? - Rectangle's 81596
The rectangle has a perimeter of 30 cm. The ratio of its sides a: b=2:3. Calculate the sides' lengths and the rectangle's area.
- Triangle - many properties
In a right triangle ABC with a right angle at the vertex C, it is given: a = 17cm, Vc = 8 cm. Calculate the length of the sides b, c, its area S, the perimeter o, the length of the radii of the circles of the triangle circumscribed by R and inscribed r an - Circles 2
Calculate the area bounded by the circumscribed and inscribed circle in a triangle with sides 16 cm, 20 cm, and 15 cm. - The perimeter 3
The perimeter of a rectangle is 35 cm. The length ratio to its width is 3:2. Calculate the rectangle's dimensions.
