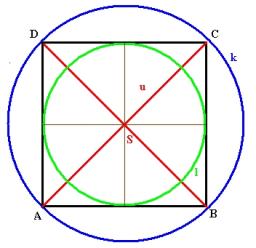
Circumscribed circle to square
Find the length of a circle circumscribing a square side of 10 cm. Compare it to the perimeter of this square.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsGrade of the word problem
Related math problems and questions:
- Rectangle
The rectangle is 21 cm long and 38 cm wide. Find the radius of the circle circumscribing the rectangle. - Circumscribing
Find the radius of the circumscribed circle to the right triangle with legs 6 cm and 3 cm. - Photo frame
A square-shaped photo with a side length of 20 cm is framed by a 4 cm wide bar. Find the external frame size of this photo (the frame is from all sides). - A cone 3
A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain. - Decagon
Calculate the area and circumference of the regular decagon when its radius of a circle circumscribing is R = 1m - PT - Pythagorean
A right triangle ABC has hypotenuse c and legs a, and b of the following lengths. Estimate the length of its remaining side and compare your estimates with your calculations. a) a = 4 cm; b = 5 cm b) a = 6.8 m; b = 9 m c) a= 8.9 m; b = 1 m d) b= 10 cm; c - Square circles
Calculate the length of the described and inscribed circle to the square ABCD with a side of 5cm.
