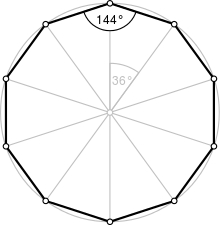
Decagon
Calculate the area and circumference of the regular decagon when its radius of a circle circumscribing is R = 1m
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Do you want to convert length units?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you want to convert length units?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Rotational motion of a cylinder
Calculate the kinetic energy of a cylindrical body of radius r= 0.08 meter and mass m= 1.5kg at time t= 5 s, if this body rotates around an axis passing through the center of the cylinder with a constant acceleration Ԑ= 5 rad/s², if at time t=. - Calculate 80793
The liquid has a specific gravity of γ = 9050 N. m-3. Calculate its specific gravity, the mass of 2 m³ of this liquid, and also of 3 m³ of this liquid. - Direct proportional
If m is proportional to n and m=5 when n=4, then what is the value of m when n=18? - ISO triangle
Calculate the area of an isosceles triangle KLM if its sides' length is in the ratio k:l:m = 4:4:3 and has a perimeter 377 mm.
- Steering 8186
What force does the driver exert when turning on the steering wheel if the steering wheel diameter is 35 cm and the torque is 3.5 N. M? - Hypotenuse 78844
Construct triangle KLM if side m=6.5cm, hypotenuse tm=4cm, height to side m: vm=3.2cm - Thermal energy
From the formula for calculating thermal energy Q=m*c*t, express t and calculate by how many °C 2kg of water must be heated to increase its energy by 126kJ
