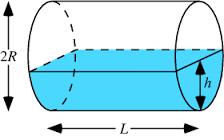
Horizontal Cylindrical Segment
How much fuel is in the horizontal cylindrical segment tank with a length of 10 m, a width of level 1 meter, and a level of 0.2 meters below the tank's upper side?
Your answer:
Your answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetrygoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Tank and water
We poured water into a cylindrical tank with 3.5 liters. If the tank's base diameter is 3 dm, how high is the water level? - Hectoliters of water
There are 942 hectoliters of water in a cylindrical tank with an inner diameter of 6 m. The water reaches two-thirds of the tank's depth. Calculate its depth. - Tank Weight Pressure Ground
The tank's weight is 36 t, and the total contact area of the belts with the ground is 4 square meters. What pressure does the tank cause on a horizontal surface? - Cableway
The cableway has a length of 1800 m. The horizontal distance between the upper and lower cable car station is 1600 m. Calculate how much meters altitude is higher upper station than at the base station. - Diesel tank
The tank has the shape of a rotating cylinder with a height of 10 m. The width of the level is 1 m, and the level is 20 cm below the top of the cylinder. How much diesel is in the tank? - Full tank
Jacob pumps a full tank into his motorcycle and leaves. On the way to the city, it consumes 11/16 tanks and back 3/5 of the rest. What percentage of the fuel will remain in the tank? - Tanks
The fire tank is cuboid in shape, with a rectangular floor measuring 13.3 m × 14.7 m. The water depth is 1.9 m. Water was pumped from the tank into barrels with a capacity of 5 hl. How many barrels would have been used if the water level in the tank
