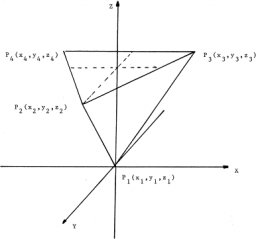
CoG center
Find the position of the center of gravity of a system of four mass points having masses, m1, m2 = 2 m1, m3 = 3 m1, and m4 = 4 m1, if they lie at the vertices of an isosceles tetrahedron. (in all cases, between adjacent material points, the distance is a=1. )
Correct answer:
Tips for related online calculators
Looking for a statistical calculator?
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
The Pythagorean theorem is the base for the right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
The Pythagorean theorem is the base for the right triangle calculator.
Calculation of an isosceles triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- statistics
- weighted average
- geometry
- analytic geometry
- vector
- solid geometry
- pyramid
- planimetrics
- Pythagorean theorem
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Gravitational 63504
Due to the force of gravity, a freely released body falls towards the Earth. The reaction to the gravitational force is of equal magnitude and acts on the Earth at its center. Explain why we do not observe the motion of the Earth towards the body. - Calculate 80793
The liquid has a specific gravity of γ = 9050 N. m-3. Calculate its specific gravity, the mass of 2 m³ of this liquid, and also of 3 m³ of this liquid. - At noon 4
At noon, the temperature was 9ºC. Between noon and 11:00 p.m., it rose by 8ºC, fell by 4ºC, rose by 3ºC, and then fell by 8ºC. What was the temperature at 11:00 p.m.? - ISO triangle
Calculate the area of an isosceles triangle KLM if its sides' length is in the ratio k:l:m = 4:4:3 and has a perimeter 377 mm.
- Function
For linear function f(x) = ax + b is f(10)=192; f(16)=170. Calculate m, if f(m) = 2008. - N points on the side
An equilateral triangle A, B, and C on each of its inner sides lies N=13 points. Find the number of all triangles whose vertices lie at given points on different sides. - Centre of mass
The vertices of triangle ABC are from the line p distances 3 cm, 4 cm, and 8 cm. Calculate the distance from the center of gravity of the triangle to line p.
