Tetraéder
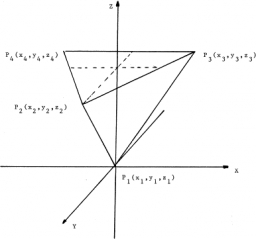
Určte polohu ťažiska sústavy štyroch hmotných bodov, ktoré majú hmotnosti, m1, m2=2m1, m3=3m1 a m4=4m1, ak ležia vo vrcholoch rovnorameného tetraédra. (vo všetkých pripadoch medzi susednými hmotnymi bodmi je vzdialenost a. )
Správna odpoveď:
Zobrazujem 3 komentáre:
Yorick929
Zdravím, môžem sa opýtať čoho výšky sú tie h, h1 a h2 a ako sme sa k nim dostali?
Vopred ďakujem za odpoveď.
Vopred ďakujem za odpoveď.
3 roky 1 Like
Dr Math
Správne riešenie pre zvolenú konfiguráciu súradnicovej sústavy: x = - 1/20, y = - sqrt (3) / 20, z = 3 * sqrt (6) / 10.
Poznámka: výška pravidelného tetraédra h = a * sqrt (6) / 3.
Poznámka: výška pravidelného tetraédra h = a * sqrt (6) / 3.
Tipy na súvisiace online kalkulačky
Hľadáte štatistickú kalkulačku?
Dva vektory určené veľkosťami a vzájomným uhlom sčíta naša kalkulačka sčítania vektorov.
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Vypočet rovnoramenného trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Dva vektory určené veľkosťami a vzájomným uhlom sčíta naša kalkulačka sčítania vektorov.
Pytagorova veta je základ výpočtov aj kalkulačky pravouhlého trojuholníka.
Vypočet rovnoramenného trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- štatistika
- vážený priemer
- geometria
- analytická geometria
- vektor
- stereometria
- ihlan
- planimetria
- Pytagorova veta
- trojuholník
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Ťažisko
Hmotné body sú rozložené v priestore nasledovne - zadané súradnice v priestore a ich hmotnosti. Nájdite polohu ťažiska tejto sústavy hmotných bodov: A1 [-15; -17; 11] m1 = 80 kg A2 [-16; -13; -5] m2 = 99 kg A - Úsečka
Úsečka je daná dvoma bodmi L[-10, -14] a M[-13, -4]. Vypočítajte súradnice bodu na úsečke, ktorý leží v 3/4 vzdialenosti medzi L a M. - Dosadenie do výrazu-vzorca
Dosaď za premenné a urči hodnotu výrazu: a) x+y+2x-3y. x=1, y = 2 b) a+5b-a+4b. a=8, b=-8 c) mn-5mn+6mn. M=-3, n=-4 d) k+10m+5k-6m+13km. k=1, m=0 - Poloha ťažiska
Na konci valcovej tyče dĺžky 0,8m je pripojena guľa s polomerom 0,1m tak, že jej stred leží na pozdĺžnej osi tyče. Obidve telesa sú z rovnakého rovnorodého materiálu. Guľa je dvakrát ťažšia ako tyč. Určte polohu ťažiska tejto sústavy telies.
- 2. Newtonov zákon
Aká stála brzdná sila je potrebná, aby sa automobil hmotnosti 1 tona zastavil za 10 sekúnd, ak ide rýchlosťou 50km/h? - Dosadením 3165
Určite hodnotu výrazu dosadením za premenné a = 5, b = 2, x = 3, y = 1: k = 4ab + 1/2 ab - 14 l= x² + 2xy + y² m= 5b³ - 4b² - Škola 3
V škole je m učební. V desiatich učebniach je po 36 stoličiek, v ostatných je po 34 stoličiek. Urč vzťah pomocou ktorého vypočítaš počet vsetkých stoličiek v triedach skoly. Vypočítaj pre m=11.
