Surveyors
Surveyors mark 4 points on the globe's surface so their distances are the same. What is their distance from each other?
Correct answer:
Showing 1 comment:
Petr
Theme - problem of a tetrahedron (4 vertices). The sphere - circumsphere (Earth) is described by this tetrahedron and we are looking from its radius to the side length. From formula.
Tips for related online calculators
Do you want to convert length units?
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- North Pole
What is the shortest distance across the globe's surface on a scale of 1:1,000,000 from the equator to the North Pole? - Determine 8133
Determine the distance between two places, M, and N, between which there is an obstacle so that place N is not visible from place M. The angles MAN = 130°, NBM = 109°, and the distances |AM| = 54, |BM| = 60, while the points A, B, and M lie on one straigh - Half-planes 36831
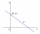The line p and the two inner points of one of the half-planes determined by the line p are given. Find point X on the line p so that the sum of its distances from points A and B is the smallest. - Distances 79974
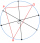The picture shows three villages, A, B, and C, and their mutual air distances. The new straight railway line is to be built so that all the villages are the same distance from the line and that this distance is the smallest possible. How far will they be
- Distances
On the way from Bratislava to Trebišov (440 km), 2 cars set off towards each other. The car from BA set off at 8:00 a.m. and the car from Trebišov at 9:00 a.m. They met at 11:00 a.m., the car from Trebišov traveled 25 km less than the second car each hour - Distance 15203
In the plane, the points A, B, and C are given 3 cm apart, and they do not lie in the same straight line. Mark the set of all points whose distance from all three points is less than or equal to 2.5 cm. - Against each other
From two points, A and B distant 29 km at the same time started two cars against each other at speeds 82 km/h and 72 km/h. How long do cars meet, and what distance passes each of them?
