Zememerači
Zememerači vytýčili na povrchu zemegule 4 body tak, že ich vzájomné vzdialenosti sú rovnaké. Aká je ich vzájomná vzdialenosť?
Vaša odpoveď:
Vaša odpoveď:
Zobrazujem 2 komentáre:
Petr
Priklad na tetrahedron - svorsten (4 vrcholy). Zemegula je opisana tomuto tetrahedronu a hladame z jej polomeru dlzku strany . Vzorec.
Petr
Zememerači zvyčajne meria vzdialenosť na povrchu zemegule. Hľadaná vzdialenosť je teda 4 * pí * sqrt (2) * R / 9 = cca 12 580 km. Niečo ako z Bratislavy do Santiaga de Chile. :-)
5 rokov 1 Like
Tipy na súvisiace online kalkulačky
Chcete premeniť jednotku dĺžky?
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebrastereometriaplanimetriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Daný je 4
Daný je štvorec ABCD. Na jeho uhlopriečke AC leží bod E tak, že platí vzdialenosť AB je rovná vzdialenosti AE. Aká je veľkosť uhla EBC? - Stĺp je
Stĺp je upevnený vo zvislej polohe 3 lanami, ktoré sú zachytené vo výške 3 m nad zemou. Druhé konce lán sú zakotvené na povrchu zeme vo vzdialenosti 4 m od päty stĺpa. Aké dlhé lano sa spotrebovalo na upevnenie stĺpa? - Na obrázku 5
Na obrázku sú znázornené tri obce A, B, C a ich vzájomné vzdušné vzdialenosti. Nová priamočiara želežničná trať má byť postavená tak, aby zo všetkých obcí bolo k trati rovnako ďaleko a aby táto vzdialenosť bola najmenšia možná. Ako ďaleko budú od trate? a - Aká je 16
Aká je mierka mapy, na ktorej sú zobrazené mestá Peking a Tokio vo vzdialenosti 5,1 cm? Ich skutočná vzdušná vzdialenosť je 2040 km. - Vrchol budovy
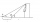Z bodov A a B na rovnom povrchu sú uhly pozorovania vrcholu budovy 25° a 37°. Ak | AB | = 57 m, vypočítajte s presnosťou na najbližší meter vzdialenosti hornej časti budovy od A a B, ak sú obidve na tej istej strane budovy. - Kábel
Pretrhol sa telefónny kabel spájajúci miesta A, B vo vzdialenosti 2,5 km. Aká je pravdepodobnosť, že sa to stalo vo vzdialenosti najviac 450 m od miesta A? - Na pozemku 2
Na pozemku tvaru obdĺžnika bude lesná školka. Jedna strana pozemku meria 12 m, druhá o 3 m viac. a) koľko metrov pletiva bude potrebných na oplotenie lesnej škôlky? b) koľko sadeníc vysadia, ak ich vzajomnà vzdialenost je 1 m a aj 1 m od plota? c) cena st
