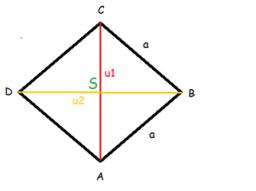
Diamond diagonals
Calculate the diamond's diagonal lengths if its area is 156 cm2 and the side length is 13 cm.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a system of equations and looking for calculator system of linear equations?
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
Do you have a system of equations and looking for calculator system of linear equations?
Do you want to convert length units?
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- system of equations
- expression of a variable from the formula
- planimetrics
- Pythagorean theorem
- area of a shape
- rhombus
- diagonal
- The Law of Sines
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- NYC block
 Bijan wants to go running during his family's vacation to New York City. To do so, he will run a neighborhood block 20 times. Bijan runs a total of 8 miles. The block has a length of 3/20 miles. Use the formula for the perimeter of the neighborhood block
Bijan wants to go running during his family's vacation to New York City. To do so, he will run a neighborhood block 20 times. Bijan runs a total of 8 miles. The block has a length of 3/20 miles. Use the formula for the perimeter of the neighborhood block - Lara's sequence
 Lara starts with a number less than 20. She divides it by 2 adds 6. She then divides this result by 3 her answer is 4.5 What number does she start with?
Lara starts with a number less than 20. She divides it by 2 adds 6. She then divides this result by 3 her answer is 4.5 What number does she start with? - One muffin
 Eight muffins and one drink cost $8.12. If the drink costs $1.24, find the cost of one muffin.
Eight muffins and one drink cost $8.12. If the drink costs $1.24, find the cost of one muffin. - Rhombus 36
 Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB.
Rhombus ABCD with side 8 cm long has diagonal BD 11.3 cm long. Find angle DAB.
- Mixed numbers equation
 4 5/9 is the same as the sum of 2 1/3 and 5/6 times a number. What is the number? Enter your answer as a mixed number in simplest form in the box.
4 5/9 is the same as the sum of 2 1/3 and 5/6 times a number. What is the number? Enter your answer as a mixed number in simplest form in the box. - 13 times
 1/3 times the sum of a number, and 2.6 is 4.9. What is the number? Enter your answer as a simplified mixed number in the box.
1/3 times the sum of a number, and 2.6 is 4.9. What is the number? Enter your answer as a simplified mixed number in the box. - The average 12
 The average of the first five numbers drawn was 2499. the first four numbers were 4165, 320, 7142, and 64. What was the fifth number?
The average of the first five numbers drawn was 2499. the first four numbers were 4165, 320, 7142, and 64. What was the fifth number? - Soup mixes
 You sell soup mixes for a fundraiser. For each soup mix you sell, the company that makes the soup receives x dollars, and you receive the remaining amount. You sell 16 soup mixes for a total of (16x+96) dollars. How much money do you receive for each soup
You sell soup mixes for a fundraiser. For each soup mix you sell, the company that makes the soup receives x dollars, and you receive the remaining amount. You sell 16 soup mixes for a total of (16x+96) dollars. How much money do you receive for each soup - Height of the box
 The box needs to have a volume of 108 ¾ cubic inches. If its width is 7 ¼ inches and its depth is 1 ¼ inches, what must its height be?
The box needs to have a volume of 108 ¾ cubic inches. If its width is 7 ¼ inches and its depth is 1 ¼ inches, what must its height be?
- Perimeter - general
 Solve: the perimeter of a triangle is 4x+1.if two of it side are(x+2) and (x-1). Find the third side.
Solve: the perimeter of a triangle is 4x+1.if two of it side are(x+2) and (x-1). Find the third side. - The proportion
 The proportion's first, second, and third terms are 4, 20, and 13. Find the fourth term.
The proportion's first, second, and third terms are 4, 20, and 13. Find the fourth term. - The mean 2
 The mean cost of 4 items was $39.96. The first item cost $28.50, the second item cost $41.25, and the third item cost $50. Find the cost of the fourth item.
The mean cost of 4 items was $39.96. The first item cost $28.50, the second item cost $41.25, and the third item cost $50. Find the cost of the fourth item. - Dimensions 83176
 If we reduce the length of the rectangle by 2 cm and the width by 1 cm, its area will decrease by 8 cm². If we increase the length of the rectangle by 1 cm and the width by 2 cm, then its content will increase by 13 cm². What were the original dimensions
If we reduce the length of the rectangle by 2 cm and the width by 1 cm, its area will decrease by 8 cm². If we increase the length of the rectangle by 1 cm and the width by 2 cm, then its content will increase by 13 cm². What were the original dimensions - Correct mean and CV
 For a group of 100 students, the mean and coefficient of variation of their marks were found to be 60 and 25, respectively. Later, it was found that the scores 45 and 70 were wrongly entered as 40 and 27. Find the corrected mean and coefficient of variati
For a group of 100 students, the mean and coefficient of variation of their marks were found to be 60 and 25, respectively. Later, it was found that the scores 45 and 70 were wrongly entered as 40 and 27. Find the corrected mean and coefficient of variati
- The capacitor
 The parallel square plates of a 4.5µF Teflon capacitor are 3.2 mm apart. What is the area of the plate?
The parallel square plates of a 4.5µF Teflon capacitor are 3.2 mm apart. What is the area of the plate? - Sides ratio and angles
 In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC.
In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC. - The enrolment 2
 The enrolment at a school has increased from 1400 learners to 1600 learners over 5 years. What is the percentage increase in enrolment?
The enrolment at a school has increased from 1400 learners to 1600 learners over 5 years. What is the percentage increase in enrolment?
