Analytic geometry - practice problems - page 7 of 14
Number of problems found: 268
- Geometric 34741
What geometric shape do all points in the plane have the same distance from a given point in the plane? - Perpendicular projection
Determine the distance of point B[1, -3] from the perpendicular projection of point A[3, -2] on a straight line 2 x + y + 1 = 0. - Vertex points
Suppose the following points of a triangle: P(-12,6), Q(4,0), R(-8,-6). Graph the triangle. Find the triangle area. - Direction vector The line p is given by the point P [- 0,5; 1] and the direction vector s = (1,5; - 3) determines: A) value of parameter t for points X [- 1,5; 3], Y [1; - 2] lines p B) whether the points R [0,5; - 1], S [1,5; 3] lie on the line p C) parametric equations
- Place vector
Place the vector AB if A (3, -1), B (5,3) in point C (1,3) so that AB = CO. - Ascend vs. descent Which function is growing? a) y = 2-x b) y = 20 c) y = (x + 2). (-5) d) y = x-2
- Coordinates 32183
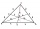The triangle ABC is given in the plane. A (-3,5), B (2,3), C (-1, -2) write the coordinates of the vectors u, v, w if u = AB, v = AC, and w = BC. Enter the coordinates of the centers of the lines SAB (..), SAC (...), SBC (. ..) - General line equations In all examples, write the GENERAL EQUATION OF a line that is given in some way. A) the line is given parametrically: x = - 4 + 2p, y = 2 - 3p B) the slope form gives the line: y = 3x - 1 C) the line is given by two points: A [3; -3], B [-5; 2] D) the lin
- The tangent line
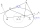Find the tangent line of the ellipse 9x² + 16y² = 144 with slope k = -1. - Tangents to ellipse Find the magnitude of the angle at which the ellipse x² + 5 y² = 5 is visible from the point P[5, 1].
- The intersection of the diagonals
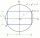In the rectangular coordinate system, a rectangle ABCD is drawn. These coordinates determine the vertices of the rectangle: A = (2.2) B = (8.2) C = (8.6) D = (2.6) Find the coordinates of the intersection of the diagonals of the ABCD rectangle. - There
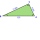There is a triangle ABC: A (-2,3), B (4, -1), C (2,5). Determine the general equations of the lines on which they lie: a) AB side, b) height to side c, c) Axis of the AB side, d) median ta to side a - Isosceles triangle
In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C. - Three points
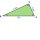Three points, K (-3; 2), L (-1; 4), and M (3, -4), are given. Find out: (a) whether the triangle KLM is right b) calculate the length of the line to the k side c) write the coordinates of the vector LM d) write the directional form of the KM side e) write - Calculate 8
Calculate the coordinates of point B axially symmetrical with point A[-1, -3] along a straight line p : x + y - 2 = 0. - Calculate 7
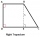Calculate the height of the trapezoid ABCD, where the coordinates of vertices are: A[2, 1], B[8, 5], C[5, 5] and D[2, 3] - Perpendicular lines
Points A(1,2), B(4,-2) and C(3,-2) are given. Find the parametric equations of the line that: a) It passes through point C and is parallel to the line AB, b) It passes through point C and is perpendicular to line AB. - Equation of the circle
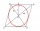Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4]. - Points in space
There are n points, of which no three lie on one line and no four lies on one plane. How many planes can be guided by these points? How many planes are there if there are five times more than the given points? - Vector v4
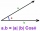Find the vector v4 perpendicular to the vectors v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) and v3 = (0, 0, 1, 1)
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
