Basic operations and concepts - math word problems - page 210 of 322
Number of problems found: 6439
- Two-meter 3473
 A tree with an unknown height casts a shadow 18 m long at a time, while a two-meter pole casts a shadow of 2.4 m. How tall is the tree?
A tree with an unknown height casts a shadow 18 m long at a time, while a two-meter pole casts a shadow of 2.4 m. How tall is the tree? - Numbered
 In the past, passengers in public transport vehicles marked such single-use tickets, which had 9 numbered boxes, a certain number of which were punched with a marker. A) In how many different ways could the ticket be marked if 3 boxes were punched? B) How
In the past, passengers in public transport vehicles marked such single-use tickets, which had 9 numbered boxes, a certain number of which were punched with a marker. A) In how many different ways could the ticket be marked if 3 boxes were punched? B) How - Light bulbs
 You are in a room with 3 switches. In the next room, there are 3 switched off classic light bulbs in table lamps, each switch belongs to a light bulb. You cannot see from one room to the other. How do you find out which switch belongs to which light bulb
You are in a room with 3 switches. In the next room, there are 3 switched off classic light bulbs in table lamps, each switch belongs to a light bulb. You cannot see from one room to the other. How do you find out which switch belongs to which light bulb - Cinema
 How many ways can 11 free tickets to the premiere of "Jáchyme throw it in the machine" be divided between 6 pensioners?
How many ways can 11 free tickets to the premiere of "Jáchyme throw it in the machine" be divided between 6 pensioners? - Differently 69514
 Gabika wants to wear pants, a blouse, a skirt, and a T-shirt to the party. She has two pairs of pants, 3 blouses, 3 skirts, and 4 T-shirts to choose from. How many parties can she attend if everyone wants to go dressed differently?
Gabika wants to wear pants, a blouse, a skirt, and a T-shirt to the party. She has two pairs of pants, 3 blouses, 3 skirts, and 4 T-shirts to choose from. How many parties can she attend if everyone wants to go dressed differently? - Different 66944
 It was Tibor's birthday, and he bought 8 different cookies for his friends (Horalky, Tatanky, Kávenky, Attack, Mila, Anita, Mäta, Lina). He put them all in a box, and each friend could choose two pieces. Tanya chose first. Which two cookies could Táňa cho
It was Tibor's birthday, and he bought 8 different cookies for his friends (Horalky, Tatanky, Kávenky, Attack, Mila, Anita, Mäta, Lina). He put them all in a box, and each friend could choose two pieces. Tanya chose first. Which two cookies could Táňa cho - Five-digit 8357
 How many five-digit numbers can you create from the numbers 1,2,3,4,5,6 if 1 and 2 must always be next to each other? We cannot repeat the digits.
How many five-digit numbers can you create from the numbers 1,2,3,4,5,6 if 1 and 2 must always be next to each other? We cannot repeat the digits. - Participated 8264
 Classes 1B, 2A, and 3C, participated in the volleyball tournament. How many ways could they take first, second, or third place? What is the probability that 1B will end before 2A class?
Classes 1B, 2A, and 3C, participated in the volleyball tournament. How many ways could they take first, second, or third place? What is the probability that 1B will end before 2A class? - Inflation and deposits
 A client deposits 100,000 euros in XYZ bank for a term deposit with an interest rate of 4% pa (per annum). After six months, you went to get the money. How much did he have in his account with the described half-yearly interest? PS When you deposit money
A client deposits 100,000 euros in XYZ bank for a term deposit with an interest rate of 4% pa (per annum). After six months, you went to get the money. How much did he have in his account with the described half-yearly interest? PS When you deposit money - Distances 79974
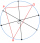 The picture shows three villages, A, B, and C, and their mutual air distances. The new straight railway line is to be built so that all the villages are the same distance from the line and that this distance is the smallest possible. How far will they be
The picture shows three villages, A, B, and C, and their mutual air distances. The new straight railway line is to be built so that all the villages are the same distance from the line and that this distance is the smallest possible. How far will they be - Lecturers 6099
 Three lecturers will create 75 tasks in two and a half days. In how many days will it take at least five lecturers to create enough exercises for the exercise book, which should contain 300 exercises? (we assume that all tutors are equally efficient and w
Three lecturers will create 75 tasks in two and a half days. In how many days will it take at least five lecturers to create enough exercises for the exercise book, which should contain 300 exercises? (we assume that all tutors are equally efficient and w - Part-timers 6436
 Five part-timers ship all goods from the warehouse in 12 days. Calculate how long it would take to bring twice as many goods out of the warehouse to part-timers if their number increased by 140%.
Five part-timers ship all goods from the warehouse in 12 days. Calculate how long it would take to bring twice as many goods out of the warehouse to part-timers if their number increased by 140%. - Maintaining 5136
 Petr succumbed to a bank's tempting offer, opened an account, and deposited CZK 1,051 into it. The account bore interest at 1.4%, credited once a year. The fee for maintaining this account was only CZK 140 per year. After seven years, he enjoyed how his d
Petr succumbed to a bank's tempting offer, opened an account, and deposited CZK 1,051 into it. The account bore interest at 1.4%, credited once a year. The fee for maintaining this account was only CZK 140 per year. After seven years, he enjoyed how his d - TV diagonal
 A diagonal TV is 0.56 m long. How big is the television screen if the aspect ratio is 16:9?
A diagonal TV is 0.56 m long. How big is the television screen if the aspect ratio is 16:9? - Similarity 26441
 How long a shadow casts a building 15 m high if the shadow of a meter rod is 90 cm? Sketch - similarity.
How long a shadow casts a building 15 m high if the shadow of a meter rod is 90 cm? Sketch - similarity. - Karolína
 Carolina chose five bodies from the kit - white, blue, and gray cubes, a blue cylinder, and a white triangular prism. How many different roof towers can be built one by one if all the blue bodies (cube and cylinder) are not placed on top?
Carolina chose five bodies from the kit - white, blue, and gray cubes, a blue cylinder, and a white triangular prism. How many different roof towers can be built one by one if all the blue bodies (cube and cylinder) are not placed on top? - Shadow
 A meter pole perpendicular to the ground throws a shadow of 40 cm long. The house throws a shadow 6 meters long. What is the height of the house?
A meter pole perpendicular to the ground throws a shadow of 40 cm long. The house throws a shadow 6 meters long. What is the height of the house? - Driver
 The driver of the supply car reckoned that at the average speed of 72 km/h arrived at the warehouse for 1 1/4 hours. After 30 km, however, he unintentionally drove to the gas station and had ten minutes delay. At what average speed would you have to go th
The driver of the supply car reckoned that at the average speed of 72 km/h arrived at the warehouse for 1 1/4 hours. After 30 km, however, he unintentionally drove to the gas station and had ten minutes delay. At what average speed would you have to go th - Individual 65004
 In the computer game, you need to collect 5 objects in the room: a sword, a ring, a picture, a key, and a coin. It depends on the order in which we collect the individual objects. If the order is wrong, we will lose a life. How many are all in order?
In the computer game, you need to collect 5 objects in the room: a sword, a ring, a picture, a key, and a coin. It depends on the order in which we collect the individual objects. If the order is wrong, we will lose a life. How many are all in order? - Single-digit 7302
 Four different digits were on the four cards, one of which was zero. Vojta composed the largest four-digit number from the cards, and Martin the smallest four-digit number. Adam wrote the difference between Vojtov's and Martin's numbers on the board. Then
Four different digits were on the four cards, one of which was zero. Vojta composed the largest four-digit number from the cards, and Martin the smallest four-digit number. Adam wrote the difference between Vojtov's and Martin's numbers on the board. Then
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
