Basic operations and concepts - math word problems - page 209 of 323
Number of problems found: 6446
- Similarity coefficient
Given triangle ABC with sides a = 12 cm b = 9 cm c = 7 cm and triangle DEF with sides d = 8.4 cm, e = 6.3 cm f = 4.9 cm Find out if triangles ABC and DEF are similar if so, write the similarity coefficient and according to which sentence they are similar - Tree shadow length
How long is the shadow of a tree 7.6 m high, and the shadow of a 190 cm high road sign is 3.3 m long? - Shadows At the park, a young woman who is 1.72 meters tall casts a 3.5 meters shadow at a certain hour. What is the height of a tree in the park that, at the same time, casts a 12.3 meters shadow?
- Inscribed triangle
A circle is an inscribed triangle, and its vertices divide the circle into three arcs. The length of the arcs is in the ratio 2:3:7. Find the interior angles of a triangle. - Circumferential angle
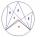Vertices of the triangle ΔABC lay on the circle and are divided into arcs in the ratio 10:8:7. Determine the size of the angles of the triangle ΔABC. - Garage
There are two laths in the garage opposite one another: one 2 meters long and the second 3 meters long. They fall against each other and stay against the opposite walls of the garage. Both laths cross 70 cm above the garage floor. How wide is the garage? - Wagons
We have six wagons: two white, two blue, and two red. We assemble trains from them; wagons of the same color are exactly the same, so if we change only two white wagons on a train, it's still the same train because I don't know any difference. How many di - Seven-segmet
Lenka is amused that he punched a calculator (seven-segment display) number and used only digits 2 to 9. Some numbers have the property that She again gave their image in the axial or central symmetry some number. Determine the maximum number of three-dig - Cinema
How many ways can 11 free tickets to the premiere of "Jáchyme throw it in the machine" be divided between 6 pensioners? - Dance pair duration
Thirty-two boys and 34 girls came to the dance. How many different dance pairs can they make, given that each team is given: they can only dance for 1 minute and then take turns in 5 seconds? Calculate how long the dance evening would last for all the pai - Tree Height Shadow Length
A man 1.65 m tall casts a shadow of 1.25 m. How tall is the tree whose shadow is in debt 2.58 m? - Two trains
Through the bridge, long l = 240m, the train passes through the constant speed at time t1 = 21s. A train running along the traffic lights at the edge of the bridge passes the same speed at t2 = 9s. a) What speed v did the train go? b) How long did a train - Karim
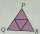Karim uses a photocopier to enlarge the triangle PQR diagram by 150%. a) Write the ratio of the length of P' Q' to the length of PQ. b) Is the ratio of the length P 'R' to the length PR equal to the ratio of the length P 'Q' to the length PQ? c) Use your - A cliff
A line from the top of a cliff to the ground passes just over the top of a pole 5 ft high. It meets the ground at a point 8 ft from the base of the pole. The point is 93 ft from the base of the cliff. How high is the cliff? - Two doctors
Doctor A will determine the correct diagnosis with a probability of 89% and doctor B with a probability of 75%. Calculate the probability of proper diagnosis if both doctors diagnose the patient. - Film premiere
How can you distribute 40 cinema tickets to 15 people? - Karolína
Carolina chose five bodies from the kit - white, blue, and gray cubes, a blue cylinder, and a white triangular prism. How many different roof towers can be built one by one if all the blue bodies (cube and cylinder) are not placed on top? - Desks
A class has 20 students. The classroom consists of 20 desks, with four desks in each of 5 different rows. Amy, Bob, Chloe, and David are all friends and would like to sit in the same row. How many possible seating arrangements exist, such as Amy, Bob, Chl - Gabika party outfits
Gabika wants to wear pants, a blouse, a skirt, and a T-shirt to the party. She has two pairs of pants, 3 blouses, 3 skirts, and 4 T-shirts to choose from. How many parties can she attend if everyone wants to go dressed differently? - Student pair selection
The coach must choose two students from Sam, Jura, Emma, Dan, and Nika to go to the competition. He knows them well and knows that Samo will only go with Jura or Ema, and Dano will not go with Ema. How many pairs does the trainer have to choose from?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
