Basic operations and concepts - math word problems - page 208 of 322
Number of problems found: 6439
- Three roads
 The three boys moved from start to finish on three different routes, A, B, and C, always simultaneously. Adam drove road A 1500 m long on a scooter. Blake walked route B 600 m long on foot. Cyril got on a scooter on route C after a 90 m walk, then he left
The three boys moved from start to finish on three different routes, A, B, and C, always simultaneously. Adam drove road A 1500 m long on a scooter. Blake walked route B 600 m long on foot. Cyril got on a scooter on route C after a 90 m walk, then he left - Wedding guests
 Fifteen wedding guests could not agree on who would stand in the wedding photo. The groom suggested that all possible sets of wedding guests be made in the photographs.
Fifteen wedding guests could not agree on who would stand in the wedding photo. The groom suggested that all possible sets of wedding guests be made in the photographs. - The chimney
 The chimney casts a shadow 45 meters long. The one-meter-long rod standing perpendicular to the ground has a shadow 90 cm long. Calculate the height of the chimney.
The chimney casts a shadow 45 meters long. The one-meter-long rod standing perpendicular to the ground has a shadow 90 cm long. Calculate the height of the chimney. - Trapezium diagonals
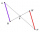 It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC.
It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC. - Display case
 Place a glass shelf at the height of 1m from the bottom of the display case in the cabinet. How long platter will we place at this height? The display case is a rectangular triangle with 2 m and 2.5 m legs.
Place a glass shelf at the height of 1m from the bottom of the display case in the cabinet. How long platter will we place at this height? The display case is a rectangular triangle with 2 m and 2.5 m legs. - Isosceles trapezoid
 In an isosceles trapezoid KLMN, the intersection of the diagonals is marked by the letter S. Calculate the area of the trapezoid if /KS/: /SM/ = 2:1 and a triangle KSN is 14 cm².
In an isosceles trapezoid KLMN, the intersection of the diagonals is marked by the letter S. Calculate the area of the trapezoid if /KS/: /SM/ = 2:1 and a triangle KSN is 14 cm². - Triangles 81480
 Decide whether the triangles are similar. Choose between Yes/No. ∆ YUO: y= 9m, u= 17 m, o= 12 m, ∆ ZXV= z= 207 dm, x= 341 dm, v= 394 dm
Decide whether the triangles are similar. Choose between Yes/No. ∆ YUO: y= 9m, u= 17 m, o= 12 m, ∆ ZXV= z= 207 dm, x= 341 dm, v= 394 dm - Grandparents
 The grandfather set aside €1200 for savings. At the beginning of each month, he deposited €100 in the bank at an interest rate of 3%p. A. At the end of the year, he had €1,219.68 in the bank. Grandma immediately put the entire amount of €1,200 into the ba
The grandfather set aside €1200 for savings. At the beginning of each month, he deposited €100 in the bank at an interest rate of 3%p. A. At the end of the year, he had €1,219.68 in the bank. Grandma immediately put the entire amount of €1,200 into the ba - The observer - trees
 The observer sees the tops of two trees at the same angle α. It is 9 m from one tree and 21 m from the other. The trees stand on a level. How tall is the second tree if the height of the first is 6 m? Remember that the eyes of a standing person are approx
The observer sees the tops of two trees at the same angle α. It is 9 m from one tree and 21 m from the other. The trees stand on a level. How tall is the second tree if the height of the first is 6 m? Remember that the eyes of a standing person are approx - Word OPTICAL
 Find the number of possible different arrangements of the letters of the word OPTICAL such that the vowels would always be together.
Find the number of possible different arrangements of the letters of the word OPTICAL such that the vowels would always be together. - Desks
 A class has 20 students. The classroom consists of 20 desks, with four desks in each of 5 different rows. Amy, Bob, Chloe, and David are all friends and would like to sit in the same row. How many possible seating arrangements exist, such as Amy, Bob, Chl
A class has 20 students. The classroom consists of 20 desks, with four desks in each of 5 different rows. Amy, Bob, Chloe, and David are all friends and would like to sit in the same row. How many possible seating arrangements exist, such as Amy, Bob, Chl - Left-handed writer
 Eva, Lucia, Barbora, Ivana, and Slávka are good friends, so they always want to sit at one long table next to each other in biology class. How many ways can they sit if Slavka is left-handed and, therefore, always wants to sit on the left side of the tabl
Eva, Lucia, Barbora, Ivana, and Slávka are good friends, so they always want to sit at one long table next to each other in biology class. How many ways can they sit if Slavka is left-handed and, therefore, always wants to sit on the left side of the tabl - Divide
 How many different ways can three people divide seven pears and five apples?
How many different ways can three people divide seven pears and five apples? - Determine 70834
 At the same time, a vertical 2-meter pole casts a shadow of 0.85 meters. At the same time, a chimney of unknown height casts a 45m long shadow. Determine the height of the chimney.
At the same time, a vertical 2-meter pole casts a shadow of 0.85 meters. At the same time, a chimney of unknown height casts a 45m long shadow. Determine the height of the chimney. - Thales
 Thales is 1 m from the hole. The eyes are 150 cm above the ground and look into the hole with a diameter of 120 cm, as shown. Calculate the depth of the hole.
Thales is 1 m from the hole. The eyes are 150 cm above the ground and look into the hole with a diameter of 120 cm, as shown. Calculate the depth of the hole. - Shadow and light
 Nine meters height poplar tree has a shadow 16.2 meters long. How long does shadow have at the same time as Joe if he is 1,4m tall?
Nine meters height poplar tree has a shadow 16.2 meters long. How long does shadow have at the same time as Joe if he is 1,4m tall? - Competition 67314
 The coach must choose two students from Sam, Jura, Emma, Dan, and Nika to go to the competition. He knows them well and knows that Samo will only go with Jura or Ema, and Dano will not go with Ema. How many pairs does the trainer have to choose from?
The coach must choose two students from Sam, Jura, Emma, Dan, and Nika to go to the competition. He knows them well and knows that Samo will only go with Jura or Ema, and Dano will not go with Ema. How many pairs does the trainer have to choose from? - Ornamental 6532
 The gardener is to plant 6 ornamental trees. There are 8 different types of trees available. Two trees, A and B, will be planted on the left edge. How many ways can a gardener do this if all the saplings planted are to be different?
The gardener is to plant 6 ornamental trees. There are 8 different types of trees available. Two trees, A and B, will be planted on the left edge. How many ways can a gardener do this if all the saplings planted are to be different? - Shadows
 At the park, a young woman who is 1.72 meters tall casts a 3.5 meters shadow at a certain hour. What is the height of a tree in the park that, at the same time, casts a 12.3 meters shadow?
At the park, a young woman who is 1.72 meters tall casts a 3.5 meters shadow at a certain hour. What is the height of a tree in the park that, at the same time, casts a 12.3 meters shadow? - Precious metals
 From 2006-2009, the value of precious metals changed rapidly. The data in the following table represent the total rate of return (in percentage) for platinum, gold, and silver from 2006 through 2009: Year Platinum Gold Silver 2009 62.7 25.0 56.8 2008 -41.
From 2006-2009, the value of precious metals changed rapidly. The data in the following table represent the total rate of return (in percentage) for platinum, gold, and silver from 2006 through 2009: Year Platinum Gold Silver 2009 62.7 25.0 56.8 2008 -41.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
