Basic operations and concepts - math word problems - page 304 of 322
Number of problems found: 6435
- Triangular prism
The base of the perpendicular triangular prism is a rectangular triangle with a hypotenuse of 10 cm and one leg of 8 cm. The prism height is 75% of the perimeter of the base. Calculate the volume and surface of the prism. - Two bodies
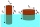The rectangle with dimensions 8 cm and 4 cm is rotated 360º first around the longer side to form the first body. Then, we similarly rotate the rectangle around the shorter side b to form a second body. Find the ratio of surfaces of the first and second bo - Dimensions of a fabric
How many m² of fabric is needed to make a tent of a regular 3-sided prism if it is necessary to count on a 2% reserve of fabric? Dimensions - 2m 1.6m and height 1.4m - Calculation 83339
The edges of a cuboid are in the ratio 1:2:3. Calculate their length if you know that the surface of the entire cuboid is S=5632 m². Then, perform a test to ensure the calculation is correct. - Function's 48141
Calculate and write in the table 10 values of the function f: y = 3x + 1, and the function's graph from them. - Pentagon
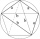The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm - Calculate 19543
Calculate the surface of a prism with a square base whose mantle is a rectangle with sides of 18cm and 8cm. How many solutions does the task have? List all solutions. - Determined 3570
There are 12 points in space, with no three lying on a straight line. How many different planes are determined by these points? - Metal balls
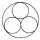Four metal balls with a diameter of 5 cm are placed in a measuring cylinder with an inner diameter of 10 cm. What is the smallest water volume to be poured into the cylinder so that all balls are below the water level? - Material consumption
The sphere-shaped reservoir has a volume of 282 hl. Calculate the material consumption in m² for its production, assuming 8% for joints and waste, and round the final result to the nearest integers. - 9 rectangles
A large rectangle is divided into 9 small rectangles. How many rectangles are there in total? - Circular 4690
The cone shell with a base radius of 20 cm and a height of 50 cm unfolds into a circular cutout. How big is the center angle of this cutout? - Bricks pyramid
How many 50cm x 32cm x 30cm bricks are needed to build a 272m x 272m x 278m pyramid? - Calculate 81935 The volume of the cuboid is 960 cm³. The lengths of the edges are in the ratio 1 : 3: 5. Calculate the surface area of the cuboid.
- Maximum of volume
The shell of the cone is formed by winding a circular section with a radius of 1. For what central angle of a given circular section will the volume of the resulting cone be maximum? - Cuboid - edges
The cuboid has dimensions in a ratio of 4:3:5. The shortest edge is 12 cm long. Find: The lengths of the remaining edges The surface of the cuboid The volume of the cuboid - Sphere and cone
Within the sphere of radius G = 33 cm, inscribe the cone with the largest volume. What is that volume, and what are the dimensions of the cone? - Alien ship
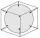The alien ship has the shape of a sphere with a radius of r = 3000m, and its crew needs the ship to carry the collected research material in a cuboid box with a square base. Determine the length of the base and (and height h) so that the box has the large - Cube zoom
If we magnify the cube's edge by 47 %, how many percent does this increase the cube's volume and surface? - Largest possible cone
It is necessary to make the largest possible cone from an iron rod in the shape of a prism with dimensions of 5.6 cm, 4.8 cm, and 7.2 cm. a) Calculate its volume. b) Calculate the waste.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
