Circle practice problems - page 47 of 50
Number of problems found: 989
- Pendulum
Calculate the pendulum's length 2 cm lower in the lowest position than in the highest position. The circular arc length to be described when moving is 20cm. - Sprinkler - irrigated area
A sprinkler is located in the park at a distance of 3m from the sidewalk. Water blasted up to a distance of max. 5m. What is the maximum length of the sidewalk it will cover? - Circle arc
Calculate the circular arc area in m² where the diameter is 263 dm and the central angle is 40°. Please result round to three decimal places. - Diameter 5668
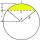The span of the arc is 247 cm, and the height of the arc is 21.5 cm. What is the diameter of the circle? - Interior angles
In a quadrilateral ABCD, whose vertices lie on some circle, the angle at vertex A is 58 degrees, and the angle at vertex B is 134 degrees. Calculate the sizes of the remaining interior angles. - Similar frustums
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - The chord
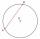A chord passing through its center is the side of the triangle inscribed in a circle. What size are a triangle's internal angles if one is 40°? - Chord circle
The circle to the (S, r = 8 cm) are different points A, B connected segment /AB/ = 12 cm. AB mark the middle of S'. Calculate |SS'|. Make the sketch. - Flakes
A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips? - Tunnel boring
How much material did they dig when cutting the 400m long tunnel? The area of the circular segment, which is the cross-section of the tunnel, is 62m². - Three segments
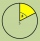The circle is divided into three segments. Segment A occupies 1/4 of the area. Segment B occupies 1/3 of the area. What part is occupied by section C? In what proportion are areas A: B: C? - Hexa pyramid
The base of the regular pyramid is a hexagon, which can be described as a circle with a radius of 2 m. Find the volume of the pyramid to be 2.5 m high. - Quarter circle
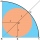What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm? - Lunes of Hippocrates
Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the - The tower
The tower of the Dean's Church in Ústí nad Labem deviates from the original vertical axis by 220 cm. Its original height was 48 m. At what height is the highest point of this tower now? Enter the result to the nearest centimeter. - Quadrilateral prism
The diagonal of section DBFH of the regular quadrilateral prism ABCDEFGH inscribes a circle with a diameter of 8 cm. What is the volume of the prism? - Circular segment
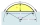A circular segment has an area of 6.04 cm², the central omega angle is 15 degrees, what is the radius? - Arc-sector
arc length = 17 cm area of sector = 55 cm² arc angle = ? the radius of the sector = ? - A goat
In the square garden of side (a), a goat is tied in the middle of one side. Calculate the length of the rope (r) so that the goat grazes exactly half the garden. If r = c * a, find the constant c. - A cell tower
A cell tower is located at coordinates (-5, -7) and has a circular range of 12 units. If Mr. XYZ is located at coordinates (4,5), will he be able to get a signal?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
