Circle practice problems - page 48 of 50
Number of problems found: 992
- Quadrilateral 8405
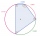 Calculate the magnitude of the largest inner angle and the deviation of the diagonals in the quadrilateral, whose vertices correspond to points 1, 5, 8, and 12 on the dial.
Calculate the magnitude of the largest inner angle and the deviation of the diagonals in the quadrilateral, whose vertices correspond to points 1, 5, 8, and 12 on the dial. - Annulus
 Two concentric circles with radii 1 and 9 surround the annular circle. This ring is inscribed with n circles that do not overlap. Determine the highest possible value of n.
Two concentric circles with radii 1 and 9 surround the annular circle. This ring is inscribed with n circles that do not overlap. Determine the highest possible value of n. - Coordinates hexagon
 The regular hexagon ABCDEF is given. Point A has coordinates [1; 3], and point D has coordinates [4; 7]. Calculate the sum of the coordinates of the center of its described circle.
The regular hexagon ABCDEF is given. Point A has coordinates [1; 3], and point D has coordinates [4; 7]. Calculate the sum of the coordinates of the center of its described circle. - Cut and cone
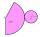 Calculate the volume of the rotation cone whose lateral surface is a circular arc with radius 15 cm and central angle 63 degrees.
Calculate the volume of the rotation cone whose lateral surface is a circular arc with radius 15 cm and central angle 63 degrees. - The cone
 The cone's lateral surface area is 4 cm², and the area of the base is 2 cm². Find the angle in degrees (deviation) of the cone sine and the cone base plane. (The cone side is the segment joining the vertex cone with any point of the base circle. All sides
The cone's lateral surface area is 4 cm², and the area of the base is 2 cm². Find the angle in degrees (deviation) of the cone sine and the cone base plane. (The cone side is the segment joining the vertex cone with any point of the base circle. All sides - Quadrilateral 82395
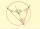 The points ABC lie on the circle k(S, r) such that the angle at B is obtuse. How large must the angle at vertex B of quadrilateral SCBA be so that this angle is three times greater than the interior angle ASC of the same quadrilateral?
The points ABC lie on the circle k(S, r) such that the angle at B is obtuse. How large must the angle at vertex B of quadrilateral SCBA be so that this angle is three times greater than the interior angle ASC of the same quadrilateral? - Flakes
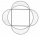 A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips?
A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips? - Quadrilateral in circle
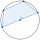 A quadrilateral is inscribed in the circle. Its vertices divide the circle in a ratio of 1:2:3:4. Find the sizes of its interior angles.
A quadrilateral is inscribed in the circle. Its vertices divide the circle in a ratio of 1:2:3:4. Find the sizes of its interior angles. - 10 pieces
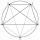 How to divide the circle into ten parts (geometrically)?
How to divide the circle into ten parts (geometrically)? - Semicircle
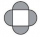 The ornament consists of one square and four dark semicircles. The area of the square is 4 cm². Find the area of one dark semicircle and round the result to hundreds.
The ornament consists of one square and four dark semicircles. The area of the square is 4 cm². Find the area of one dark semicircle and round the result to hundreds. - Circle annulus
 There are two concentric circles in the figure. The chord of the larger circle, 10 cm long, is tangent to the smaller circle. What does annulus have?
There are two concentric circles in the figure. The chord of the larger circle, 10 cm long, is tangent to the smaller circle. What does annulus have? - Circumferential 8399
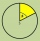 A circle with a radius r=8 cm is divided by points K and L in a ratio of 5 to 4. Calculate the sizes of the center and circumferential angles, corresponding to both arcs and the area of the larger segment.
A circle with a radius r=8 cm is divided by points K and L in a ratio of 5 to 4. Calculate the sizes of the center and circumferential angles, corresponding to both arcs and the area of the larger segment. - Circular sector
 I have a circular sector with a length of 15 cm with an unknown central angle. It is created from a circle with a radius of 5 cm. What is the central angle alpha in the circular sector?
I have a circular sector with a length of 15 cm with an unknown central angle. It is created from a circle with a radius of 5 cm. What is the central angle alpha in the circular sector? - Pavement
 Calculate the length of the pavement that runs through a circular square with a diameter of 40 m if the distance of the pavement from the center is 15 m.
Calculate the length of the pavement that runs through a circular square with a diameter of 40 m if the distance of the pavement from the center is 15 m. - Field with vegetables
 The field planted with vegetables has a rectangular isosceles triangle with a leg length of 24 m. At the triangle's vertices are rotating sprinklers with a range of 12 m. How much of the field sprinkler isn't irrigated?
The field planted with vegetables has a rectangular isosceles triangle with a leg length of 24 m. At the triangle's vertices are rotating sprinklers with a range of 12 m. How much of the field sprinkler isn't irrigated? - Rectangular trapezoid ZIMA
 I have a rectangular trapezoid ZIMA (the right angle at the top of Z. ZIMA = winter in English) ZI-7cm, ZM-5cm, AM-3.5cm, and we have to write the procedure to construct this trapezoid.
I have a rectangular trapezoid ZIMA (the right angle at the top of Z. ZIMA = winter in English) ZI-7cm, ZM-5cm, AM-3.5cm, and we have to write the procedure to construct this trapezoid. - Equation of circle 2
 Find the equation of a circle that touches the axis of y at a distance of 4 from the origin and cuts off an intercept of length 6 on the axis x.
Find the equation of a circle that touches the axis of y at a distance of 4 from the origin and cuts off an intercept of length 6 on the axis x. - The circle arc
 Calculate the span of the arc, which is part of a circle with diameter d = 11 m and its height is 5 m.
Calculate the span of the arc, which is part of a circle with diameter d = 11 m and its height is 5 m. - A chord
 In a circle radius of 6 cm, a chord is drawn 3 cm from the center. Calculate the angle subtended by the chord at the center of the circle. Hence find the length of the minor arc cut off by the chord.
In a circle radius of 6 cm, a chord is drawn 3 cm from the center. Calculate the angle subtended by the chord at the center of the circle. Hence find the length of the minor arc cut off by the chord. - Circle section
 An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a
An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
