Circular sector practice problems - page 3 of 4
Remember: Solve each problem thoughtfully and make sure to show your complete solution for every question.Number of problems found: 72
- Circle arc segment
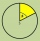 A circle with a radius r=8 cm is divided by points K and L in a ratio of 5 to 4. Calculate the sizes of the center and circumferential angles, corresponding to both arcs and the area of the larger segment.
A circle with a radius r=8 cm is divided by points K and L in a ratio of 5 to 4. Calculate the sizes of the center and circumferential angles, corresponding to both arcs and the area of the larger segment. - Circle section
 An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a
An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a - Goat
 The fenced flower bed has the shape of a regular hexagon. The tops are formed by fence posts. The fence around the flowerbed measures 60 m. A goat is tied to one of the pillars from the outside and grazes on the surrounding meadow (the goat should not ent
The fenced flower bed has the shape of a regular hexagon. The tops are formed by fence posts. The fence around the flowerbed measures 60 m. A goat is tied to one of the pillars from the outside and grazes on the surrounding meadow (the goat should not ent - Pendulum
 Calculate the pendulum's length 2 cm lower in the lowest position than in the highest position. The circular arc length to be described when moving is 20cm.
Calculate the pendulum's length 2 cm lower in the lowest position than in the highest position. The circular arc length to be described when moving is 20cm. - Sprayer grass area
 What grass area can the automatic sprayer spray if it is set to spray at an angle of 120 ° and the water sprays up to a maximum distance of 5 meters?
What grass area can the automatic sprayer spray if it is set to spray at an angle of 120 ° and the water sprays up to a maximum distance of 5 meters? - Three segments
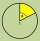 The circle is divided into three segments. Segment A occupies 1/4 of the area. Segment B occupies 1/3 of the area. What part is occupied by section C? In what proportion are areas A: B: C?
The circle is divided into three segments. Segment A occupies 1/4 of the area. Segment B occupies 1/3 of the area. What part is occupied by section C? In what proportion are areas A: B: C? - Circle diameter
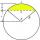 The span of the arc is 247 cm, and the height of the arc is 21.5 cm. What is the diameter of the circle?
The span of the arc is 247 cm, and the height of the arc is 21.5 cm. What is the diameter of the circle? - Circle segment
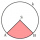 A quarter circle with a radius of 4 has the same area as a circle segment with a radius of 3. What is the magnitude of the center angle of the circle segment?
A quarter circle with a radius of 4 has the same area as a circle segment with a radius of 3. What is the magnitude of the center angle of the circle segment? - The tower
 The tower of the Dean's Church in Ústí nad Labem deviates from the original vertical axis by 220 cm. Its original height was 48 m. At what height is the highest point of this tower now? Enter the result to the nearest centimeter.
The tower of the Dean's Church in Ústí nad Labem deviates from the original vertical axis by 220 cm. Its original height was 48 m. At what height is the highest point of this tower now? Enter the result to the nearest centimeter. - Surface of the cone
 Calculate the cone's surface if its height is 8 cm and the volume is 301.44 cm³.
Calculate the cone's surface if its height is 8 cm and the volume is 301.44 cm³. - Cone Radius Sector Angle
 Determine the cone's base's radius if its shell develops into a circular section with radius "s" = 10 and center angle x = 60 °. r = ?, o =?
Determine the cone's base's radius if its shell develops into a circular section with radius "s" = 10 and center angle x = 60 °. r = ?, o =? - Spherical cap
 The spherical cap has a base radius of 8 cm and a height of 5 cm. Calculate the radius of a sphere of which this spherical cap is cut.
The spherical cap has a base radius of 8 cm and a height of 5 cm. Calculate the radius of a sphere of which this spherical cap is cut. - Lunes of Hippocrates
 Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the
Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the - Quarter circle
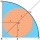 What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm?
What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm? - Mice
 Mice consumed a circular hole in a slice of cheese. The cheese is a circular cut with a radius of 20 cm and an angle of 90 degrees. What percentage of the cheese ate mice if they made 20 holes with a diameter of 2 cm?
Mice consumed a circular hole in a slice of cheese. The cheese is a circular cut with a radius of 20 cm and an angle of 90 degrees. What percentage of the cheese ate mice if they made 20 holes with a diameter of 2 cm? - Angle of the sector
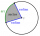 Find the angle of the sector of a circle radius of 20 units where the area is equal to the lateral area of a cone with a radius of 8 units.
Find the angle of the sector of a circle radius of 20 units where the area is equal to the lateral area of a cone with a radius of 8 units. - Flakes
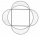 A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips?
A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips? - Spherical sector
 The spherical sector has axial section has an angle of α = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the surface of this spherical sector.
The spherical sector has axial section has an angle of α = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the surface of this spherical sector. - Semicircle
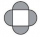 The ornament consists of one square and four dark semicircles. The area of the square is 4 cm². Find the area of one dark semicircle and round the result to hundreds.
The ornament consists of one square and four dark semicircles. The area of the square is 4 cm². Find the area of one dark semicircle and round the result to hundreds. - Arc and segment
 Calculate the length of circular arc l, the area of the circular arc S1, and the area of circular segment S2. The circle's radius is 88, and the corresponding angle is (4)/(7) π.
Calculate the length of circular arc l, the area of the circular arc S1, and the area of circular segment S2. The circle's radius is 88, and the corresponding angle is (4)/(7) π.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
