Frustum practice problems - page 2 of 3

Direction: Solve each problem carefully and show your solution in each item.

Number of problems found: 56

Frustrum - volume, area
Calculate the surface and volume of a truncated rotating cone with base radii of 8 cm and 4 cm and a height of 5 cm.
Hexagon cut pyramid
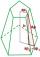Calculate the volume of a regular 6-sided cut pyramid if the bottom edge is 30 cm, the top edge is 12 cm, and the side edge length is 41 cm.
Quadrangular pyramid
Calculate the surface area and volume of a regular quadrangular pyramid: sides of bases (bottom, top): a1 = 18 cm, a2 = 6cm angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.) S =? , V =?
Truncated cone
Calculate the volume of a truncated cone with base radiuses r₁=19 cm, r₂ = 11 cm, and height v = 5 cm.
Truncated pyramid
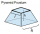The concrete pedestal in a regular quadrilateral truncated pyramid has a height of 12 cm; the pedestal edges have lengths of 2.4 and 1.6 dm. Calculate the surface of the base.
Quadrilateral 81385
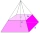A regular quadrilateral pyramid with base edge length a = 15cm and height v = 21cm is given. We draw two planes parallel to the base, dividing the height of the pyramid into three equal parts. Calculate the ratio of the volumes of the 3 bodies created.
An Elizabethan collar
An Elizabethan collar is used to prevent an animal from irritating a wound. The angle between the opening (diameter 6 inches) with a 16-inch diameter and the side of the collar is 53 degrees. Find the surface area of the collar shown.
The truncated
The truncated rotating cone has bases with radii r1 = 8 cm, r2 = 4 cm, and height v = 5 cm. What is the volume of the cone from which the truncated cone originated?
Truncated pyramid
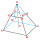Find the volume and surface area of a regular quadrilateral truncated pyramid if base lengths a1 = 17 cm, a2 = 5 cm, and height v = 8 cm.
Truncated 43851
The pit is a regular truncated 4-sided pyramid, with 14 m and 10 m base edges and a depth of 6m. Calculate how much m³ of soil was removed when we dug this pit.
A concrete pedestal
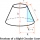A concrete pedestal has the shape of a right circular cone and a height of 2.5 feet. The diameters of the upper and lower bases are 3 feet and 5 feet, respectively. Determine the pedestal's lateral surface area, total surface area, and volume.
4B - truncated pyramid
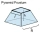Calculate the volume of a regular truncated quadrilateral pyramid if the base edges are 10cm and 4cm and the height of the side wall is 5cm.
Truncated pyramid
Find the volume of a regular 4-sided truncated pyramid if a1 = 14 cm, a2 = 8 cm, and the angle that the side wall with the base is 42 degrees.
Slant surface
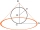The surface of the rotating cone and its base area is in the ratio 18:5. Determine the volume of the cone if its body height is 12 cm.
Truncated pyramid
The truncated regular quadrilateral pyramid has a volume of 74 cm³, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base.
Truncated pyramid
How many cubic meters is the volume of a regular four-sided truncated pyramid with edges of one meter and 60 cm and a high of 250 mm?
Quadrilateral 81033
The foundations of a regular truncated quadrilateral pyramid are squares. The lengths of the sides differ by 6 dm. Body height is 7 dm. The body volume is 1813 dm³. Calculate the lengths of the edges of both bases.
Side deviation
Frustum has the base radii of the figures r1 and r2: r1> r2, r2 = s, and if the side deviation from the base plane is 60°. Express the surface and volume of the cone frustum using its side s.
Top-open tank
The top-open tank resembles a truncated rotating cone, standing on a smaller base. Its volume is 465 m³, and the bases' radii are 4 m and 3 m. Find the tank's depth.
Quadrilateral 5814
Calculate the surface area and volume of a regular quadrilateral truncated pyramid if the base edges are 87 cm and 64 cm and the wall height is 49 cm.

Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.