Geometry - math word problems - page 74 of 162
Number of problems found: 3238
- Two walls
 Calculate the surface area of a cube in m² if you know that the area of its two walls is 72 dm².
Calculate the surface area of a cube in m² if you know that the area of its two walls is 72 dm². - Regular hexagonal pyramid
 Calculate the height of a regular hexagonal pyramid with a base edge of 5 cm and a wall height of w = 20cm. Sketch a picture.
Calculate the height of a regular hexagonal pyramid with a base edge of 5 cm and a wall height of w = 20cm. Sketch a picture. - Hexagon
 Calculate the surface area of the regular hexagonal prism, whose base edge a = 12cm and side edge b = 3 dm.
Calculate the surface area of the regular hexagonal prism, whose base edge a = 12cm and side edge b = 3 dm. - The plaster cast
 The plaster cast has the shape of a regular quadrilateral pyramid. The cover consists of four equilateral triangles with a 5 m side. Calculate its volume and surface area.
The plaster cast has the shape of a regular quadrilateral pyramid. The cover consists of four equilateral triangles with a 5 m side. Calculate its volume and surface area. - Iron ball
 The iron ball weighs 100 kilograms. Calculate the volume, radius, and surface if the iron's density is h = 7.6g/cm³.
The iron ball weighs 100 kilograms. Calculate the volume, radius, and surface if the iron's density is h = 7.6g/cm³. - The aquarium
 The aquarium has a capacity of 18 liters. When the square bottom is 28 2/3 cm long, what is its height?
The aquarium has a capacity of 18 liters. When the square bottom is 28 2/3 cm long, what is its height? - Base of house
 Calculate the volume of the bases of a square house. If the base depth is 1.2 m, the width is 40 cm, and the outer circumference is 40.7 m.
Calculate the volume of the bases of a square house. If the base depth is 1.2 m, the width is 40 cm, and the outer circumference is 40.7 m. - Triangular prism
 Calculate the volume and surface of the triangular prism ABCDEF with the base of an isosceles triangle. Base's height is 16 cm, leg 10 cm, base height vc = 6 cm. The prism height is 9 cm.
Calculate the volume and surface of the triangular prism ABCDEF with the base of an isosceles triangle. Base's height is 16 cm, leg 10 cm, base height vc = 6 cm. The prism height is 9 cm. - Pyramid 4sides
 Calculate the volume and the surface of a regular quadrangular pyramid when the edge of the base is 4 cm long, and the pyramid's height is 7 cm.
Calculate the volume and the surface of a regular quadrangular pyramid when the edge of the base is 4 cm long, and the pyramid's height is 7 cm. - Octahedron
 All walls of the regular octahedron are identical equilateral triangles. ABCDEF octahedron edges have a length d = 6 cm. Calculate the surface area and volume of this octahedron.
All walls of the regular octahedron are identical equilateral triangles. ABCDEF octahedron edges have a length d = 6 cm. Calculate the surface area and volume of this octahedron. - Sphere
 Intersect between the plane and a sphere is a circle with a radius of 60 mm. The cone, whose base is this circle and whose apex is at the center of the sphere, has a height of 34 mm. Calculate the surface area and volume of a sphere.
Intersect between the plane and a sphere is a circle with a radius of 60 mm. The cone, whose base is this circle and whose apex is at the center of the sphere, has a height of 34 mm. Calculate the surface area and volume of a sphere. - Cut and cone
 Calculate the volume of the rotation cone whose lateral surface is a circular arc with radius 15 cm and central angle 63 degrees.
Calculate the volume of the rotation cone whose lateral surface is a circular arc with radius 15 cm and central angle 63 degrees. - Insulation
 A special rubber pipe protector is used to insulate the supply pipes of solar collectors. The product with the description DNa20, thickness 25 mm, 2 m, corresponds to insulation for pipes with a diameter of 20 mm with a rubber layer thickness of 25 mm, wh
A special rubber pipe protector is used to insulate the supply pipes of solar collectors. The product with the description DNa20, thickness 25 mm, 2 m, corresponds to insulation for pipes with a diameter of 20 mm with a rubber layer thickness of 25 mm, wh - Hectoliters 25821
 The cistern of the public water supply has a cube-shaped interior. The edge of this cube is 5 m long. a) How much water is in the reservoir when it is completely filled? (Express this volume in m³ and hectoliters. ) b) How high does the water reach in the
The cistern of the public water supply has a cube-shaped interior. The edge of this cube is 5 m long. a) How much water is in the reservoir when it is completely filled? (Express this volume in m³ and hectoliters. ) b) How high does the water reach in the - Deviation 4905
 The flower bed has the shape of a regular 4-sided pyramid. The edge of the lower plinth is 10 m, and the upper plinth is 9 m. The deviation of the side wall from the base is 45 degrees. How many plantings should be purchased if 90 are needed to plant 1 sq
The flower bed has the shape of a regular 4-sided pyramid. The edge of the lower plinth is 10 m, and the upper plinth is 9 m. The deviation of the side wall from the base is 45 degrees. How many plantings should be purchased if 90 are needed to plant 1 sq - Cuboid - box
 The box has the shape of a cuboid with dimensions of 5 cm and 30 mm. Calculate the box's height if the cuboid's volume is 0.60 dm³. Calculate the surface area of the box. (calculation of height from the volume, calculation of area from the formula, keep
The box has the shape of a cuboid with dimensions of 5 cm and 30 mm. Calculate the box's height if the cuboid's volume is 0.60 dm³. Calculate the surface area of the box. (calculation of height from the volume, calculation of area from the formula, keep - The pot
 The pot is a cylinder with a volume of V = 7l and an inner diameter of d = 20cm. Find its depth.
The pot is a cylinder with a volume of V = 7l and an inner diameter of d = 20cm. Find its depth. - The chimney
 The chimney casts a shadow 45 meters long. The one-meter-long rod standing perpendicular to the ground has a shadow 90 cm long. Calculate the height of the chimney.
The chimney casts a shadow 45 meters long. The one-meter-long rod standing perpendicular to the ground has a shadow 90 cm long. Calculate the height of the chimney. - Trapezium diagonals
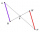 It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC.
It is given trapezium ABCD with bases | AB | = 12 cm, |CD| = 8 cm. Point S is the intersection of the diagonals for which |AS| is 6 cm long. Calculate the length of the full diagonal AC. - Display case
 Place a glass shelf at the height of 1m from the bottom of the display case in the cabinet. How long platter will we place at this height? The display case is a rectangular triangle with 2 m and 2.5 m legs.
Place a glass shelf at the height of 1m from the bottom of the display case in the cabinet. How long platter will we place at this height? The display case is a rectangular triangle with 2 m and 2.5 m legs.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
