Goniometry and trigonometry - practice problems - page 4 of 31
Number of problems found: 619
- Calculate 2575
Calculate the area and height of the rhombic cover plate to which the following applies: d (BC) = 60 cm, angle BAD = 45 °, angle ADB = 90 °. - Diagonals 5113
The diagonals in diamond KLMN are 10 cm and 6 cm long. Determine the angle size that the longer diagonal makes with the side of the diamond. - Parallelogram - two sides
The parallelogram has the sides a = 25.3 b = 13.8, and the angle closed by the sides is a = 72°. Calculate the area of the parallelogram. - Rectangular
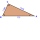Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K, and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle - A trapezoid
A trapezoid with a base length of a = 36.6 cm, with angles α = 60°, β = 48°, and the height of the trapezoid is 20 cm. Calculate the lengths of the other sides of the trapezoid. - Nonagon
Calculate the area and perimeter of a regular nonagon if its radius of the inscribed circle is r = 10cm. - Components 2565
The component is a regular decagon with a side of 2 cm. Its material weight of 1 m² of sheet metal is 24 kg. What is the weight of 200 components?
- Tree
How tall is the tree observed at the visual angle 45°? If I stand 3 m from the tree, my eyes are two meters above the ground. - How far
From the top of a lighthouse 145 ft above sea level, the angle of depression of a boat is 29°. How far is the boat from the lighthouse? - Right angled triangle 3
Side b = 1.5, hypotenuse angle A = 70 degrees, Angle B = 20 degrees. Find the length of its unknown sides. - Cable car 2
The cable car rises at an angle of 16° and connects the upper and lower station with an altitude difference of 1082 m. How long is the cable car's track? - Rectangle
Calculate the length of the side HM and diagonal EM of rectangle EHMQ when given: |QM| = 29 cm and angle ∠ EHQ = 36 degrees. - Tourist 39691
How far from the lookout tower, 48 m high, did the tourist stand if he saw its top at an angle of 40°? - Flowerbed
The flowerbed has the shape of an obtuse isosceles triangle. The arm has a size of 5.5 meters, and an angle opposite the base size is 94°. What is the distance from the base to the opposite vertex? - Kites
Boys run kites on a cable of 68 meters long. What is the kite altitude if the angle from the horizontal plane is 72°?
- Triangle SAA
The triangle has one side long 23 m, and its two internal angles are 60°. Calculate the perimeter and area of the triangle. - Calculate 5121
Calculate the height of the tree - data - from a distance of 41m at an angle of 15 degrees. I will see it in its entirety. - Circumscribed 22713
Calculate the circumference and the area of a regular ten-angle polygon if the radius of the circumscribed circle r = 20 cm. - Difference 4749
How big a difference in altitude will the cable car overcome when it rises 1200 m at a 70-degree angle? - Angle of diagonals
Calculate a rectangle's perimeter and area if its diagonal is 14 cm and the diagonals form an angle of 130°.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
