Physical quantity - math word problems - page 327 of 346
Number of problems found: 6901
- The volleyball ball
 The volleyball ball can have a circumference of at least 650 max 750 mm after inflation. What air volume can this ball hold if its circumference is the average of the minimum and maximum inflation of the ball?
The volleyball ball can have a circumference of at least 650 max 750 mm after inflation. What air volume can this ball hold if its circumference is the average of the minimum and maximum inflation of the ball? - Cylindrical magnets
 Calculate the magnetic field energy of a cylindrical coil with 400 turns, a length of 0.4 m, and a radius of 20 mm. A current of 3A passes through the coil. (µo = 4π 10-7 H/m)
Calculate the magnetic field energy of a cylindrical coil with 400 turns, a length of 0.4 m, and a radius of 20 mm. A current of 3A passes through the coil. (µo = 4π 10-7 H/m) - Carousel for children
 There are 5 seats evenly distributed on the children's carousel in the shape of a circle. What kind the arm of the carousel (connecting the center of the carousel to the seat) is long if the distance between with two seats is 1.2m?
There are 5 seats evenly distributed on the children's carousel in the shape of a circle. What kind the arm of the carousel (connecting the center of the carousel to the seat) is long if the distance between with two seats is 1.2m? - Seats on carousel
 There are 12 seats evenly distributed on the children's carousel in the shape of a circle. How long is the arm of the carousel (connecting the center of the carousel to the seat) if the distance between the two seats is 1.5m?
There are 12 seats evenly distributed on the children's carousel in the shape of a circle. How long is the arm of the carousel (connecting the center of the carousel to the seat) if the distance between the two seats is 1.5m? - The rescue helicopter
 The rescue helicopter is above the landing site at a height of 180m. The rescue operation site can be seen from here at a depth angle of 52°40'. How far will the helicopter land from the rescue site?
The rescue helicopter is above the landing site at a height of 180m. The rescue operation site can be seen from here at a depth angle of 52°40'. How far will the helicopter land from the rescue site? - Steps
 Find the height between the two floors if you know that the number of steps between the two floors is 18, the gradient is 30º, and the step length is 28.6 cm. Report the result in centimeters to the nearest centimeter.
Find the height between the two floors if you know that the number of steps between the two floors is 18, the gradient is 30º, and the step length is 28.6 cm. Report the result in centimeters to the nearest centimeter. - Unit resistance
 What is the resistance of a two-conductor line 10 m long made of 4.0 mm² aluminum wire?
What is the resistance of a two-conductor line 10 m long made of 4.0 mm² aluminum wire? - Cylinder 72094
 The tank has the shape of a rotating cylinder with a base radius of 6 m reach. Water flows at a speed of 2 liters per second for 3 hours. To what height does the water in the tank?
The tank has the shape of a rotating cylinder with a base radius of 6 m reach. Water flows at a speed of 2 liters per second for 3 hours. To what height does the water in the tank? - Observation 17433
 The aircraft flying just above point A can be seen from observation B, 2,400 meters away from point A, at an altitude of 52°30'. How high does the plane fly?
The aircraft flying just above point A can be seen from observation B, 2,400 meters away from point A, at an altitude of 52°30'. How high does the plane fly? - Components 2565
 The component is a regular decagon with a side of 2 cm. Its material weight of 1 m² of sheet metal is 24 kg. What is the weight of 200 components?
The component is a regular decagon with a side of 2 cm. Its material weight of 1 m² of sheet metal is 24 kg. What is the weight of 200 components? - Average speed
 A car traveled from city A to city B at a speed of 40 km/h, then from B to C at 60 km/h, and finally from C to D at 50 km/h. Calculate the car's average speed over the entire route from A to D if the distance from A to B is 20% of the total distance and f
A car traveled from city A to city B at a speed of 40 km/h, then from B to C at 60 km/h, and finally from C to D at 50 km/h. Calculate the car's average speed over the entire route from A to D if the distance from A to B is 20% of the total distance and f - The shooter
 The shooter shoots at the target, assuming that the individual shots are independent of each other and the probability of hitting them is 0.2. The shooter fires until he hits the target for the first time, then stops firing. (a) What is the most likely nu
The shooter shoots at the target, assuming that the individual shots are independent of each other and the probability of hitting them is 0.2. The shooter fires until he hits the target for the first time, then stops firing. (a) What is the most likely nu - Triangle SAS
 Calculate the triangle area and perimeter if the two sides are 46 m and 33 m long and angle them clamped is 170 °.
Calculate the triangle area and perimeter if the two sides are 46 m and 33 m long and angle them clamped is 170 °. - Iceberg
 What is the surface area of a 50 cm iceberg (in the shape of a cuboid) that can carry a man with luggage with a total weight of 120 kg?
What is the surface area of a 50 cm iceberg (in the shape of a cuboid) that can carry a man with luggage with a total weight of 120 kg? - Angles of elevation
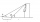 From points A and B on level ground, the angles of elevation of the top of a building are 25° and 37°, respectively. If |AB| = 57m, calculate, to the nearest meter, the distances of the top of the building from A and B if they are both on the same side of
From points A and B on level ground, the angles of elevation of the top of a building are 25° and 37°, respectively. If |AB| = 57m, calculate, to the nearest meter, the distances of the top of the building from A and B if they are both on the same side of - Two boats
 Two boats are located from a height of 150m above the lake's surface at depth angles of 57° and 39°. Find the distance of both boats if the sighting device and both ships are in a plane perpendicular to the lake's surface.
Two boats are located from a height of 150m above the lake's surface at depth angles of 57° and 39°. Find the distance of both boats if the sighting device and both ships are in a plane perpendicular to the lake's surface. - Bridge across the river
 The width of the river is 89 m. For terrain reasons, the bridge deviates from a common perpendicular to both banks by an angle of 12° 30 '. Calculate how many meters the bridge is longer than the river.
The width of the river is 89 m. For terrain reasons, the bridge deviates from a common perpendicular to both banks by an angle of 12° 30 '. Calculate how many meters the bridge is longer than the river. - Elevation angles
 Two endpoints distant 240 m are inclined at an angle of 18°15'. The top of the mountain can be seen at elevation angles of 43° and 51° from its. How high is the mountain?
Two endpoints distant 240 m are inclined at an angle of 18°15'. The top of the mountain can be seen at elevation angles of 43° and 51° from its. How high is the mountain? - Diagonals 5113
 The diagonals in diamond KLMN are 10 cm and 6 cm long. Determine the angle size that the longer diagonal makes with the side of the diamond.
The diagonals in diamond KLMN are 10 cm and 6 cm long. Determine the angle size that the longer diagonal makes with the side of the diamond. - Icerink
 A rectangular rink with 68.7 m and 561 dm dimensions must be covered with a layer of ice 4.2 cm thick. How many liters of water is necessary for ice formation when the ice volume is 9.7% greater than the volume of water?
A rectangular rink with 68.7 m and 561 dm dimensions must be covered with a layer of ice 4.2 cm thick. How many liters of water is necessary for ice formation when the ice volume is 9.7% greater than the volume of water?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
