Planimetrics - math word problems - page 157 of 185
Number of problems found: 3685
- 10 pieces
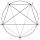 How to divide the circle into ten parts (geometrically)?
How to divide the circle into ten parts (geometrically)? - Hypotenuse 65744
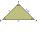 Construct a right triangle ABC with the hypotenuse AB: a) | AB | = 72 mm, | BC | = 51 mm b) | AB | = 58 mm, | AC | = 42 mm
Construct a right triangle ABC with the hypotenuse AB: a) | AB | = 72 mm, | BC | = 51 mm b) | AB | = 58 mm, | AC | = 42 mm - Scale
 The swimming pool is long 50 m and 30 m wide. The city's plan is shown as a rectangle with an area 2.4 cm². What scale is the city plan?
The swimming pool is long 50 m and 30 m wide. The city's plan is shown as a rectangle with an area 2.4 cm². What scale is the city plan? - In an
 In an ABCD square, n interior points are chosen on each side. Find the number of all triangles whose vertices X, Y, and Z lie at these points and on different sides of the square.
In an ABCD square, n interior points are chosen on each side. Find the number of all triangles whose vertices X, Y, and Z lie at these points and on different sides of the square. - Scale plan
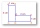 On a 1:150 scale plan, the garden is 20 cm wide and 30 cm long. What is the actual width and length of the garden? (in meters)
On a 1:150 scale plan, the garden is 20 cm wide and 30 cm long. What is the actual width and length of the garden? (in meters) - Construct 83156
 Construct 2 circles so that their centers are 5 cm apart and: and they had no common touch b- they had a common point They had 2 points in common.
Construct 2 circles so that their centers are 5 cm apart and: and they had no common touch b- they had a common point They had 2 points in common. - Sss triangle 2
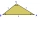 Construct triangle ABC in which |AB|=5cm, |AC|=6cm and |BC|=9cm
Construct triangle ABC in which |AB|=5cm, |AC|=6cm and |BC|=9cm - Circumscribed iso triangle
 Construct an isosceles triangle if a given circle circumscribed with a radius r = 2.6 cm is given.
Construct an isosceles triangle if a given circle circumscribed with a radius r = 2.6 cm is given. - Square-shaped 81445
 The area of the square-shaped room on the drawing with a scale of 1:150 is 6 cm square. Determine the actual area of the room in square meters.
The area of the square-shaped room on the drawing with a scale of 1:150 is 6 cm square. Determine the actual area of the room in square meters. - Magnitudes 80788
 The minute hand is three times longer than the second hand. In what ratio are the magnitudes of the velocities of their endpoints?
The minute hand is three times longer than the second hand. In what ratio are the magnitudes of the velocities of their endpoints? - Shooter
 The probability that a good shooter hits the center of the target circle No. I is 0.13. The probability that the target hit the inner circle II is 0.58. What is the probability that it hits the target circle I or II?
The probability that a good shooter hits the center of the target circle No. I is 0.13. The probability that the target hit the inner circle II is 0.58. What is the probability that it hits the target circle I or II? - Distance 22043
 There is a given circle k (S, 4 cm) and a line p. If the distance of point S from line p is less than 4 cm, is the line p called?
There is a given circle k (S, 4 cm) and a line p. If the distance of point S from line p is less than 4 cm, is the line p called? - North + west
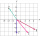 Find the magnitude of the resultant of the given vectors: vector 1:2 m/s, north vector 2:7 m/s, west
Find the magnitude of the resultant of the given vectors: vector 1:2 m/s, north vector 2:7 m/s, west - Square 58873
 Draw a square so that its sides do not lie on the lines of the square grid
Draw a square so that its sides do not lie on the lines of the square grid - Construction of trapezoid
 Construct a trapezoid if b = 4cm, c = 7cm, d = 4,5cm, v = 3 cm (Procedure, discussion, sketch, analysis, construction)
Construct a trapezoid if b = 4cm, c = 7cm, d = 4,5cm, v = 3 cm (Procedure, discussion, sketch, analysis, construction) - Map
 Forest has an area of 77 ha. How much area is occupied by forest on the map at scale 1:10000?
Forest has an area of 77 ha. How much area is occupied by forest on the map at scale 1:10000? - The triangle
 Three vertices give the triangle: A [0.0] B [-4.2] C [-6.0] Calculate V (intersection of heights), T (center of gravity), O - the center of a circle circumscribed
Three vertices give the triangle: A [0.0] B [-4.2] C [-6.0] Calculate V (intersection of heights), T (center of gravity), O - the center of a circle circumscribed - Arbitrary 6486
 Draw an arbitrary triangle ABC and a line o to have exactly 2 points in common with the triangle.
Draw an arbitrary triangle ABC and a line o to have exactly 2 points in common with the triangle. - Diagonals
 Draw a square ABCD whose diagonals have a length of 6 cm.
Draw a square ABCD whose diagonals have a length of 6 cm. - Different points
 Mark 4 different points O, P, R. S. Mark of line OP, OR, OS. Measure the marked lines.
Mark 4 different points O, P, R. S. Mark of line OP, OR, OS. Measure the marked lines.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
