Planimetrics - math word problems - page 72 of 185
Number of problems found: 3686
- Tree trunk
 From the tree trunk, the diameter at the narrower end is 28 cm, and a beam of the square cross-section is to be made. Calculate the longest side of the largest possible square cross-section.
From the tree trunk, the diameter at the narrower end is 28 cm, and a beam of the square cross-section is to be made. Calculate the longest side of the largest possible square cross-section. - Quadrilateral 80729
 Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD.
Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD. - Triangles 80492
 The sum of the lengths of the three segments is 140mm. Name at least 2 triplets of segment lengths from which we can construct a triangle. Construct triangles
The sum of the lengths of the three segments is 140mm. Name at least 2 triplets of segment lengths from which we can construct a triangle. Construct triangles - Needed 69374
 How many square tiles with an edge of 10 cm are needed to line a wall 2.4 m long to a height of 1.6 m?
How many square tiles with an edge of 10 cm are needed to line a wall 2.4 m long to a height of 1.6 m? - Diamond-shaped 69324
 How many meters is more mesh needed to fence a plot of parallels with dimensions of 50m and 40m than to fence a plot of diamond-shaped land, the side of which is 40m long?
How many meters is more mesh needed to fence a plot of parallels with dimensions of 50m and 40m than to fence a plot of diamond-shaped land, the side of which is 40m long? - Calculate 65014
 The radius of the circle is 5.5 cm. The height is 2.3 cm, which is the chord's distance. How can we calculate the length of the string?
The radius of the circle is 5.5 cm. The height is 2.3 cm, which is the chord's distance. How can we calculate the length of the string? - Rectangular 26091
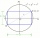 The circular running track has a diameter of 130 meters. Can a rectangular surface with dimensions of 12m and 50m be grassed inside the circle?
The circular running track has a diameter of 130 meters. Can a rectangular surface with dimensions of 12m and 50m be grassed inside the circle? - Playground
 On the special playground, there are 81 square sectors, each with a side of 5 m. How many players can fit on the playground if each player needs a 75 m² area to play?
On the special playground, there are 81 square sectors, each with a side of 5 m. How many players can fit on the playground if each player needs a 75 m² area to play? - Surrounded 13601
 The letter H is part of a square surrounded by a circle with a diameter of 42 cm. Is a fabric 1 meter long enough to make this letter? Neglect the thickness of the fabric.
The letter H is part of a square surrounded by a circle with a diameter of 42 cm. Is a fabric 1 meter long enough to make this letter? Neglect the thickness of the fabric. - Trapezoid - legs
 Determine the trapezoid area with bases 84 and 47; the height is 4 shorter than its leg.
Determine the trapezoid area with bases 84 and 47; the height is 4 shorter than its leg. - Circles 2
 Calculate the area bounded by the circumscribed and inscribed circle in a triangle with sides 29 cm, 16 cm, and 21 cm.
Calculate the area bounded by the circumscribed and inscribed circle in a triangle with sides 29 cm, 16 cm, and 21 cm. - RT a-b-x
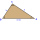 There is a right triangle with legs long a, b, and hypotenuse long x. Given that a = 6 cm and b = 9 cm, work out x. Give your answer as an exact surd.
There is a right triangle with legs long a, b, and hypotenuse long x. Given that a = 6 cm and b = 9 cm, work out x. Give your answer as an exact surd. - ABC gifts
 Arthur had 30 dollars to spend on three gifts. He spent 9 3/4 dollars on gift A and 4 1/2 dollars on gift B. How much money did he have left for gift C?
Arthur had 30 dollars to spend on three gifts. He spent 9 3/4 dollars on gift A and 4 1/2 dollars on gift B. How much money did he have left for gift C? - A piece 5
 A piece of cloth is laid at the center of a table 80 cm long and 60 cm wide, and it leaves 5 cm all around. Find the area which is not covered by the piece of cloth.
A piece of cloth is laid at the center of a table 80 cm long and 60 cm wide, and it leaves 5 cm all around. Find the area which is not covered by the piece of cloth. - A land 2
 A land owner owns two parcels of land measuring 4 2/5 hectares and 6 1/5 hectares. He sells 3/4 of the total land. How many hectares of land are left?
A land owner owns two parcels of land measuring 4 2/5 hectares and 6 1/5 hectares. He sells 3/4 of the total land. How many hectares of land are left? - Parallogram
 The Parallelogram base is 24 cm and high at 10 cm. How many tiles are required to cover a floor with an area of 1080 m²?
The Parallelogram base is 24 cm and high at 10 cm. How many tiles are required to cover a floor with an area of 1080 m²? - Paint cans
 How many paint cans are needed to paint the floor in two rooms measuring 6.8m x 4.5m and 6m x 3.8 m? One can cover 6 m².
How many paint cans are needed to paint the floor in two rooms measuring 6.8m x 4.5m and 6m x 3.8 m? One can cover 6 m². - Rectangle JANO
 The rectangle has side lengths | JA | = 16cm and | AN | = 12cm. Point S is the center of the JO side, and point T is the center of the JA side. Calculate the perimeter of the pentagon in cm.
The rectangle has side lengths | JA | = 16cm and | AN | = 12cm. Point S is the center of the JO side, and point T is the center of the JA side. Calculate the perimeter of the pentagon in cm. - Square area
 Complete the table and then draw each square. Provide exact lengths. Describe any problems you have. Side Length Area Square 1 1 unit² Square 2 2 units² Square 3 4 units²
Complete the table and then draw each square. Provide exact lengths. Describe any problems you have. Side Length Area Square 1 1 unit² Square 2 2 units² Square 3 4 units² - Cableway
 The cableway has a length of 1800 m. The horizontal distance between the upper and lower cable car station is 1600 m. Calculate how much meters altitude is higher upper station than at the base station.
The cableway has a length of 1800 m. The horizontal distance between the upper and lower cable car station is 1600 m. Calculate how much meters altitude is higher upper station than at the base station.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
