Planimetrics - math word problems - page 89 of 184
Number of problems found: 3676
- Unpainted 14513
 The abcd square is composed of 36 small squares. Six of them are painted. How many small squares do we still need to color so that a quarter of the area of the abcd square remains unpainted?
The abcd square is composed of 36 small squares. Six of them are painted. How many small squares do we still need to color so that a quarter of the area of the abcd square remains unpainted? - Identical 6406
 The area of 90000 m² is divided into 36 identical squares. Find the length of the side of one square (in meters).
The area of 90000 m² is divided into 36 identical squares. Find the length of the side of one square (in meters). - Centimeters 4404
 Calculate the diagonal of a square if its area is equal to 169 square centimeters.
Calculate the diagonal of a square if its area is equal to 169 square centimeters. - RT = legs, circle
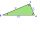 One leg of a right triangle ABC has length a= 14 cm and the radius of the circle inscribed in this triangle r= 5 cm. Calculate the length of the hypotenuse and its other leg.
One leg of a right triangle ABC has length a= 14 cm and the radius of the circle inscribed in this triangle r= 5 cm. Calculate the length of the hypotenuse and its other leg. - Diagonals 82850
 How do I find the diagonals of a rhombus if its perimeter is 80dm and one diagonal is 2x larger than the other?
How do I find the diagonals of a rhombus if its perimeter is 80dm and one diagonal is 2x larger than the other? - Calculate 70804
 The garden is a right triangle fenced with a 364 m fence length. The shorter slope of the triangle is 26 m long. Calculate the area of this garden.
The garden is a right triangle fenced with a 364 m fence length. The shorter slope of the triangle is 26 m long. Calculate the area of this garden. - Circumference 20933
 Calculates the circumference of a circle if its area is S = 2119.5 cm².
Calculates the circumference of a circle if its area is S = 2119.5 cm². - Trapezoid
 Trapezoid ABCD a = 35 m, b=28 m c = 11 m and d = 14 m. How to calculate its area?
Trapezoid ABCD a = 35 m, b=28 m c = 11 m and d = 14 m. How to calculate its area? - Two annuluses
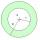 The area of the annular circle formed by two circles with a common center is 100 cm². The radius of the outer circle is equal to twice the radius of the inner circle. Determine the outside circle radius in centimeters.
The area of the annular circle formed by two circles with a common center is 100 cm². The radius of the outer circle is equal to twice the radius of the inner circle. Determine the outside circle radius in centimeters. - Calculate 39131
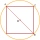 A circle describes a square with a side of 8 cm. Calculate the area of the rest of the circle if we cut out the square.
A circle describes a square with a side of 8 cm. Calculate the area of the rest of the circle if we cut out the square. - Calculated 4765
 The volume of the cylinder is calculated as V = 1/4 pi times d on the type times v. Express the average d using the volume V and the height in the cylinder. Calculate d for V = 1000 l and v = 23dm
The volume of the cylinder is calculated as V = 1/4 pi times d on the type times v. Express the average d using the volume V and the height in the cylinder. Calculate d for V = 1000 l and v = 23dm - Calculate 4382
 Each has a width of 218 cm and an area of 10,900 cm². Calculate the height of the window.
Each has a width of 218 cm and an area of 10,900 cm². Calculate the height of the window. - General triangle
 Given a general triangle ABC. Its perimeter is 30 cm, with side a=2 cm longer than side b and 5 cm shorter than side c. Determine the area of the triangle.
Given a general triangle ABC. Its perimeter is 30 cm, with side a=2 cm longer than side b and 5 cm shorter than side c. Determine the area of the triangle. - Square and circles
 The square in the picture has a side length of a = 20 cm. Circular arcs have centers at the vertices of the square. Calculate the areas of the colored unit. Express area using side a.
The square in the picture has a side length of a = 20 cm. Circular arcs have centers at the vertices of the square. Calculate the areas of the colored unit. Express area using side a. - Two chords
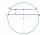 In a circle with a radius of 8.5 cm, two parallel chords are constructed, the lengths of which are 9 cm and 12 cm. Find the distance of the chords in a circle.
In a circle with a radius of 8.5 cm, two parallel chords are constructed, the lengths of which are 9 cm and 12 cm. Find the distance of the chords in a circle. - Trapezoid 15
 The area of a trapezoid is 266. What value is x if bases b1 is 2x-3, b2 is 2x+1, and height h is x+4
The area of a trapezoid is 266. What value is x if bases b1 is 2x-3, b2 is 2x+1, and height h is x+4 - Paper squares
 We should cut the paper rectangle measuring 69 cm and 46 cm into as many squares as possible. Calculate the lengths of squares and their number.
We should cut the paper rectangle measuring 69 cm and 46 cm into as many squares as possible. Calculate the lengths of squares and their number. - Median
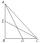 In the ABC triangle is given side a=10 cm and median to side a: ta= 13 cm, and angle gamma 90°. Calculate the length of the median to side b (tb).
In the ABC triangle is given side a=10 cm and median to side a: ta= 13 cm, and angle gamma 90°. Calculate the length of the median to side b (tb). - Flowerbed 2
 Around the square flower bed in a park is a sidewalk about 1.3 m wide. The area of this sidewalk is 246 m². What is the area of the flowerbed?
Around the square flower bed in a park is a sidewalk about 1.3 m wide. The area of this sidewalk is 246 m². What is the area of the flowerbed? - Playground 79454
 In Kocourkov, they decided to build a children's playground and volleyball courts. The volleyball court will have dimensions of 18m x 19m. The playground will have a square face. The area of both fields will be the same. What will be the dimensions of t
In Kocourkov, they decided to build a children's playground and volleyball courts. The volleyball court will have dimensions of 18m x 19m. The playground will have a square face. The area of both fields will be the same. What will be the dimensions of t
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
