Pythagorean theorem - math word problems - page 32 of 73
Number of problems found: 1449
- Face of the house
 How tall is the roof of a house in the shape of an isosceles triangle with a base length of 8 meters and an arm 5 meters long?
How tall is the roof of a house in the shape of an isosceles triangle with a base length of 8 meters and an arm 5 meters long? - Described circle to rectangle
 The rectangle with 6 cm and 4 cm sides was a circumscribed circle. What part of the circle area determined by the circumscribed circle occupies a rectangle? Express in perctentages(%).
The rectangle with 6 cm and 4 cm sides was a circumscribed circle. What part of the circle area determined by the circumscribed circle occupies a rectangle? Express in perctentages(%). - Broken tree
 The tree was 35 meters high. The tree broke at a height of 10 m above the ground. Top, but does not fall off. It is refuted on the ground. How far from the base of the tree lay its peak?
The tree was 35 meters high. The tree broke at a height of 10 m above the ground. Top, but does not fall off. It is refuted on the ground. How far from the base of the tree lay its peak? - Percentage 82591
 A new path is to lead through Mr. Milan's garden – diagonally. By what percentage of the area of the park will it decrease? The length is 23.8 m, the width is 16.7 m, and the road width is 6 m.
A new path is to lead through Mr. Milan's garden – diagonally. By what percentage of the area of the park will it decrease? The length is 23.8 m, the width is 16.7 m, and the road width is 6 m. - Intersection 81457
 Two cars started from the right-angled intersection of two roads. The first at a speed of 80 km/h and the second at a speed of 60 km/h. How fast are they moving away from each other?
Two cars started from the right-angled intersection of two roads. The first at a speed of 80 km/h and the second at a speed of 60 km/h. How fast are they moving away from each other? - Distance 79874
 The mast is 190m high and is attached to six ropes which are anchored in the ground at a distance of 20m from the base of the mast. How many meters of rope were needed?
The mast is 190m high and is attached to six ropes which are anchored in the ground at a distance of 20m from the base of the mast. How many meters of rope were needed? - Monkeys 9751
 Two monkeys were sitting on a tree, one at the top and the other 10 cubits from the ground. Both wanted to drink from a spring that was 40 cubits away. One monkey jumped to the spring from the top and flew the same path as the other monkey. How long did t
Two monkeys were sitting on a tree, one at the top and the other 10 cubits from the ground. Both wanted to drink from a spring that was 40 cubits away. One monkey jumped to the spring from the top and flew the same path as the other monkey. How long did t - Circumscribed 2671
 The circle's radius circumscribed by the rectangle is 5 cm, and one side of the rectangle is 6 cm long. Calculate the length of the other side and the area of the rectangle.
The circle's radius circumscribed by the rectangle is 5 cm, and one side of the rectangle is 6 cm long. Calculate the length of the other side and the area of the rectangle. - IS trapezoid
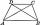 Calculate the length of diagonal u and height v of isosceles trapezoid ABCD, whose bases have lengths a = |AB| = 37 cm, c = |CD| = 29 cm and legs b = d = |BC| = |AD| = 28 cm.
Calculate the length of diagonal u and height v of isosceles trapezoid ABCD, whose bases have lengths a = |AB| = 37 cm, c = |CD| = 29 cm and legs b = d = |BC| = |AD| = 28 cm. - Chord 24
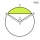 A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments?
A chord with length t = r times the square root of two divides a circle with radius r into two circular segments. What is the ratio of the areas of these segments? - Rectangle ABCD
 The rectangle ABCD is given whose | AB | = 5 cm, | AC | = 8 cm, ∢ | CAB | = 30°. How long is the other side, and what is its area?
The rectangle ABCD is given whose | AB | = 5 cm, | AC | = 8 cm, ∢ | CAB | = 30°. How long is the other side, and what is its area? - Five circles
 On the line segment CD = 6, there are five circles with one radius at regular intervals. Find the lengths of the lines AD, AF, AG, BD, and CE.
On the line segment CD = 6, there are five circles with one radius at regular intervals. Find the lengths of the lines AD, AF, AG, BD, and CE. - The garden
 The garden has the shape of a rectangular trapezium. The bases have lengths of 27 meters and 36 meters, and the trapezoid's height is 12 meters. Calculate how much a fence will cost this garden if one meter costs 1.5 €.
The garden has the shape of a rectangular trapezium. The bases have lengths of 27 meters and 36 meters, and the trapezoid's height is 12 meters. Calculate how much a fence will cost this garden if one meter costs 1.5 €. - The sides
 The sides of the rectangle are in a ratio of 3:5, and its circumference measures 72 cm. Calculate: a) the size of both sides of the rectangle b) the area of the rectangle c) the length of the diagonals
The sides of the rectangle are in a ratio of 3:5, and its circumference measures 72 cm. Calculate: a) the size of both sides of the rectangle b) the area of the rectangle c) the length of the diagonals - Diagonals in diamond
 In the rhombus, a = 160 cm and alpha = 60 degrees are given. Calculate the length of the diagonals.
In the rhombus, a = 160 cm and alpha = 60 degrees are given. Calculate the length of the diagonals. - Recursion squares
 In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 20 cm. Calculate: a) the sum of peri
In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 20 cm. Calculate: a) the sum of peri - Hypotenuses 83154
 In a right-angled triangle ABC with a right angle at the vertex C, the magnitudes of the hypotenuses are given ta=5, tb=2√10. Calculate the side sizes of triangle ABC and the circle's radius described by this triangle.
In a right-angled triangle ABC with a right angle at the vertex C, the magnitudes of the hypotenuses are given ta=5, tb=2√10. Calculate the side sizes of triangle ABC and the circle's radius described by this triangle. - Intersections 68784
 The figure shows the circles k₁(S₁; r1=9 cm) and k₂(S2; r2 = 5 cm). Their intersections determine a common chord t 8 cm long. Calculate the center distance |S₁ S₂| in cm to two decimal places.
The figure shows the circles k₁(S₁; r1=9 cm) and k₂(S2; r2 = 5 cm). Their intersections determine a common chord t 8 cm long. Calculate the center distance |S₁ S₂| in cm to two decimal places. - Magnitudes 64704
 The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '. - Dedicated 62673
 The street lamp is 5.5 m high. It suddenly stopped shining. How long do ladders need workers if they know that dedicated lamps can be placed at a distance of 18 dm at the bottom?
The street lamp is 5.5 m high. It suddenly stopped shining. How long do ladders need workers if they know that dedicated lamps can be placed at a distance of 18 dm at the bottom?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
