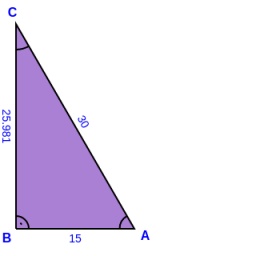
Right triangle eq2
Find the lengths of the sides and the angles in the right triangle. Given area S = 210 and perimeter o = 70.
Correct answer:
Tips to related online calculators
Looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Pythagorean theorem is the base for the right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Pythagorean theorem is the base for the right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Triangle in a square
In a square ABCD with side a = 6 cm, point E is the center of side AB, and point F is the center of side BC. Calculate the size of all angles of the triangle DEF and the lengths of its sides. - Right triangle
Calculate the missing side b and interior angles, perimeter, and area of a right triangle if a=10 cm and hypotenuse c = 16 cm. - Trapezoid MO
The rectangular trapezoid ABCD with the right angle at point B, |AC| = 12, |CD| = 8, diagonals are perpendicular to each other. Calculate the perimeter and area of the trapezoid. - The aspect ratio
The aspect ratio of the rectangular triangle is 13: 12: 5. Calculate the internal angles of the triangle. - Ratio iso triangle
The ratio of the sides of an isosceles triangle is 7:6:7 Find the base angle to the nearest answer correct to 3 significant figure. - Largest angle of the triangle
Calculate the largest angle of the triangle whose sides have the sizes: 2a, 3/2a, 3a - Circular railway
The railway connects in a circular arc the points A, B, and C, whose distances are | AB | = 30 km, AC = 95 km, BC | = 70 km. How long will the track from A to C? - Right
Determine angles of the right triangle with the hypotenuse c and legs a, b, if: 3a +4b = 4.9c - Deviation of the lines
Find the deviation of the lines AG, BH in the ABCDEFGH box-cuboid, if given | AB | = 3cm, | AD | = 2cm, | AE | = 4cm - Angle in RT
Determine the size of the smallest internal angle of a right triangle whose sides constitutes sizes consecutive members of arithmetic progressions. - Decagon
Calculate the area and circumference of the regular decagon when its radius of a circle circumscribing is R = 1m - Roof angle
The roof of the house has the shape of an isosceles triangle with arms 4 m long and the size of the base 6 m. How big an angle alpha does its roof make? - Pentagon
Calculate the length of the side, circumference, and area of a regular pentagon, which is inscribed in a circle with a radius r = 6 cm. - Diamond diagonals
Find the diamond diagonal's lengths if the area is 156 cm² and side is 13 cm long. - Four sides of trapezoid
In the trapezoid ABCD is |AB| = 73.6 mm; |BC| = 57 mm; |CD| = 60 mm; |AD| = 58.6 mm. Calculate the size of its interior angles. - Triangle ABC v2
Area of the triangle is 12 cm square. Angle ACB = 30º , AC = (x + 2) cm, BC = x cm. Calculate the value of x. - Ratio in trapezium
The height v and the base a, c in the trapezoid ABCD are in the ratio 1: 6: 3, its content S = 324 square cm. Peak angle B = 35 degrees. Determine the perimeter of the trapezoid
