Pythagorean theorem - math word problems - page 51 of 73
Number of problems found: 1451
- Felix
 Calculate how much land Felix Baumgartner saw after jumping from $km km above the ground. The radius of the Earth is $RR.
Calculate how much land Felix Baumgartner saw after jumping from $km km above the ground. The radius of the Earth is $RR. - Digging a pit
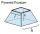 The pit has the shape of a regular quadrilateral truncated pyramid. The edges of the bases are 14m and 10m long. The sidewalls form an angle of 135° with a smaller base. Find how many m³ of soil were excavated when digging the pit.
The pit has the shape of a regular quadrilateral truncated pyramid. The edges of the bases are 14m and 10m long. The sidewalls form an angle of 135° with a smaller base. Find how many m³ of soil were excavated when digging the pit. - Pine wood
 We cut a carved beam from a pine trunk 6 m long and 35 cm in diameter. The beam's cross-section is in the shape of a square, which has the greatest area. Calculate the length of the sides of a square. Calculate the volume of lumber in cubic meters.
We cut a carved beam from a pine trunk 6 m long and 35 cm in diameter. The beam's cross-section is in the shape of a square, which has the greatest area. Calculate the length of the sides of a square. Calculate the volume of lumber in cubic meters. - Hexagonal pyramid
 The pyramid's base is a regular hexagon, which can be circumscribed in a circle with a radius of 1 meter. Calculate the volume of a pyramid 2.5 meters high.
The pyramid's base is a regular hexagon, which can be circumscribed in a circle with a radius of 1 meter. Calculate the volume of a pyramid 2.5 meters high. - Tower
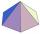 The top of the tower is a regular hexagonal pyramid with a base edge 5.7 meters long and a height 7 meters. How many m² of the sheet is required to cover the top of the tower? We must add 4% of metal for waste.
The top of the tower is a regular hexagonal pyramid with a base edge 5.7 meters long and a height 7 meters. How many m² of the sheet is required to cover the top of the tower? We must add 4% of metal for waste. - Four-sided 7910
 The roof of the recreation cottage has the shape of a regular four-sided pyramid with a height of 8m and a base edge of 4m. How much ℅ went to folds and joints, and 75.9 square meters of sheet metal were used to cover the roof?
The roof of the recreation cottage has the shape of a regular four-sided pyramid with a height of 8m and a base edge of 4m. How much ℅ went to folds and joints, and 75.9 square meters of sheet metal were used to cover the roof? - Calculate cuboid, diagonals
 The volume of a cuboid with a square base is 64 cm3, and the body diagonal deviation from the base's plane is 45 degrees. Calculate its surface area.
The volume of a cuboid with a square base is 64 cm3, and the body diagonal deviation from the base's plane is 45 degrees. Calculate its surface area. - Tower roof
 The tower's roof is a regular 4-sided pyramid with a height of 4m and an edge of the base of 6m. 25% of the roof covering was found to be damaged. How many square meters of coverage are needed to repair the roof?
The tower's roof is a regular 4-sided pyramid with a height of 4m and an edge of the base of 6m. 25% of the roof covering was found to be damaged. How many square meters of coverage are needed to repair the roof? - Triangular pyramid
 Calculate the volume of a regular triangular pyramid with edge length a = 12cm and pyramid height v = 20cm.
Calculate the volume of a regular triangular pyramid with edge length a = 12cm and pyramid height v = 20cm. - Triangular prism
 The base of the perpendicular triangular prism is a rectangular triangle with a hypotenuse of 10 cm and one leg of 8 cm. The prism height is 75% of the perimeter of the base. Calculate the volume and surface of the prism.
The base of the perpendicular triangular prism is a rectangular triangle with a hypotenuse of 10 cm and one leg of 8 cm. The prism height is 75% of the perimeter of the base. Calculate the volume and surface of the prism. - Dimensions of a fabric
 How many m² of fabric is needed to make a tent of a regular 3-sided prism if it is necessary to count on a 2% reserve of fabric? Dimensions - 2m 1.6m and height 1.4m
How many m² of fabric is needed to make a tent of a regular 3-sided prism if it is necessary to count on a 2% reserve of fabric? Dimensions - 2m 1.6m and height 1.4m - Cube from sphere
 What largest surface area (in cm²) can have a cube that we cut out of a sphere with a radius 26 cm?
What largest surface area (in cm²) can have a cube that we cut out of a sphere with a radius 26 cm? - Bottles of juice
 How many 2-liter bottles of juice need to buy if you want to transfer the juice to 50 pitchers' rotary cone shape with a diameter of 24 cm and a base side length of 1.5 dm?
How many 2-liter bottles of juice need to buy if you want to transfer the juice to 50 pitchers' rotary cone shape with a diameter of 24 cm and a base side length of 1.5 dm? - Prism
 A right-angled prism, whose base is a right triangle with leg a = 3 cm and hypotenuse c = 6 cm, has the same volume as a cube with an edge length of 1 dm. a) Find the height of the prism b) Calculate the surface of the prism c) What percentage of the cube
A right-angled prism, whose base is a right triangle with leg a = 3 cm and hypotenuse c = 6 cm, has the same volume as a cube with an edge length of 1 dm. a) Find the height of the prism b) Calculate the surface of the prism c) What percentage of the cube - Cone A2V
 The cone's surface in the plane is a circular arc with a central angle of 126° and an area of 415 cm². Calculate the volume of a cone.
The cone's surface in the plane is a circular arc with a central angle of 126° and an area of 415 cm². Calculate the volume of a cone. - Side wall planes
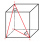 Find the volume and surface of a cuboid whose side c is 30 cm long and whose body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Find the volume and surface of a cuboid whose side c is 30 cm long and whose body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - Quadrilateral 33143
 The roof of the prefabricated holiday cottage has the shape of a regular quadrilateral pyramid with a length of the base edge of 8 meters and a height of 9 m. How many square meters of cardboard are needed to cover the roof?
The roof of the prefabricated holiday cottage has the shape of a regular quadrilateral pyramid with a length of the base edge of 8 meters and a height of 9 m. How many square meters of cardboard are needed to cover the roof? - Administrator 23801
 The administrator of the castle is trying to estimate how many square meters of sheet metal will be needed for the new roof of the tower. The roof has the shape of a cone. The castle administrator knows that the tower's diameter is 4.6 meters and its heig
The administrator of the castle is trying to estimate how many square meters of sheet metal will be needed for the new roof of the tower. The roof has the shape of a cone. The castle administrator knows that the tower's diameter is 4.6 meters and its heig - Tank
 In the middle of a cylindrical tank with a bottom diameter of 479 cm, there is a standing rod 34 cm above the water surface. If we bank the rod, its end reaches the water's surface just by the tank wall. How deep is the tank?
In the middle of a cylindrical tank with a bottom diameter of 479 cm, there is a standing rod 34 cm above the water surface. If we bank the rod, its end reaches the water's surface just by the tank wall. How deep is the tank? - Dimensions - crate
 A wooden crate with dimensions d=3m, e=4m, and f=3m was placed in a transport container with dimensions a=10 m, b=4m, and c=3m. What is the maximum length of a straight, rigid rod of negligible diameter that can still be placed in the container in this si
A wooden crate with dimensions d=3m, e=4m, and f=3m was placed in a transport container with dimensions a=10 m, b=4m, and c=3m. What is the maximum length of a straight, rigid rod of negligible diameter that can still be placed in the container in this si
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
