Pythagorean theorem - math word problems - page 57 of 73
Number of problems found: 1453
- Ratio-cuboid
 The lengths of the edges of the cuboid are in the ratio 2:3:6. Its body diagonal is 14 cm long. Calculate the volume and surface area of the cuboid.
The lengths of the edges of the cuboid are in the ratio 2:3:6. Its body diagonal is 14 cm long. Calculate the volume and surface area of the cuboid. - Calculate cylinder
 In the rotating cylinder, it is given: V = 120 cm3, v = 4 cm. Calculate r, S mantle.
In the rotating cylinder, it is given: V = 120 cm3, v = 4 cm. Calculate r, S mantle. - Cylinder surface
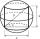 The area of the rotating cylinder shell is half the area of its surface. Calculate the surface of the cylinder if you know that the diagonal of the axial section is 5 cm.
The area of the rotating cylinder shell is half the area of its surface. Calculate the surface of the cylinder if you know that the diagonal of the axial section is 5 cm. - Rotary bodies
 The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height, v = 15 cm. Which of these two bodies has a larger surface area?
The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height, v = 15 cm. Which of these two bodies has a larger surface area? - Cuboid - volume, diagonals
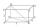 The length of the one base edge of cuboid a is 3 cm. The body diagonal is ut=13 cm, and the diagonal of the cuboid's base is u1=5 cm. What is the volume of the cuboid?
The length of the one base edge of cuboid a is 3 cm. The body diagonal is ut=13 cm, and the diagonal of the cuboid's base is u1=5 cm. What is the volume of the cuboid? - Two balls
 Two balls, one 8cm in radius and the other 6cm in radius, are placed in a cylindrical plastic container 10cm in radius. Find the volume of water necessary to cover them.
Two balls, one 8cm in radius and the other 6cm in radius, are placed in a cylindrical plastic container 10cm in radius. Find the volume of water necessary to cover them. - Tent
 Calculate how many liters of air will fit in the tent with a shield in the shape of an isosceles right triangle with legs r = 3 m long, the height = 1.5 m, and a side length d = 5 m.
Calculate how many liters of air will fit in the tent with a shield in the shape of an isosceles right triangle with legs r = 3 m long, the height = 1.5 m, and a side length d = 5 m. - Box volume
 Calculate the volume of a wooden box in the shape of a prism with the base of a rectangle if the box's width is 8 dm, the length is 14 dm, and the size of the body diagonal is 25 dm.
Calculate the volume of a wooden box in the shape of a prism with the base of a rectangle if the box's width is 8 dm, the length is 14 dm, and the size of the body diagonal is 25 dm. - Axial section
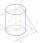 The axial section of the cylinder has a diagonal 50 cm. The shell size and base surface are in the ratio 2:5. Calculate the volume and surface area of this cylinder.
The axial section of the cylinder has a diagonal 50 cm. The shell size and base surface are in the ratio 2:5. Calculate the volume and surface area of this cylinder. - Cone and the ratio
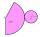 The rotational cone has a height of 59 cm, and the ratio of the base surface to the lateral surface is 10: 12. Calculate the surface of the base and the lateral surface.
The rotational cone has a height of 59 cm, and the ratio of the base surface to the lateral surface is 10: 12. Calculate the surface of the base and the lateral surface. - Elevation
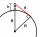 What must be an observer's elevation so that he may see an object on the Earth 866 km away? Assume the Earth to be a smooth sphere with a radius 6378.1 km.
What must be an observer's elevation so that he may see an object on the Earth 866 km away? Assume the Earth to be a smooth sphere with a radius 6378.1 km. - Horizon
 The top of a lighthouse is 18 m above the sea. How far away is an object just "on the horizon"? [Assume the Earth is a sphere of radius 6378.1 km.]
The top of a lighthouse is 18 m above the sea. How far away is an object just "on the horizon"? [Assume the Earth is a sphere of radius 6378.1 km.] - Diagonal
 Determine the dimensions of the cuboid if it is diagonally long 60 dm and has an angle with one edge 35° and with another edge 77°.
Determine the dimensions of the cuboid if it is diagonally long 60 dm and has an angle with one edge 35° and with another edge 77°. - Pyramid roof
 3/5 of the area of the roof-shaped regular tetrahedral pyramid with base edge 9 m and height of 6 m is already covered with roofing. How many square meters still need to be covered?
3/5 of the area of the roof-shaped regular tetrahedral pyramid with base edge 9 m and height of 6 m is already covered with roofing. How many square meters still need to be covered? - The cap
 A rotating cone shapes a jester hat. Calculate how much paper is needed for the cap 53 cm high when the head circumference is 45 cm.
A rotating cone shapes a jester hat. Calculate how much paper is needed for the cap 53 cm high when the head circumference is 45 cm. - Pyramid surface
 There is a regular quadrilateral pyramid with the base edge length a = 3 cm and with the length of the side edge h = 8 cm. Please calculate its surface area and volume.
There is a regular quadrilateral pyramid with the base edge length a = 3 cm and with the length of the side edge h = 8 cm. Please calculate its surface area and volume. - 4B - truncated pyramid
 Calculate the volume of a regular truncated quadrilateral pyramid if the base edges are 10cm and 4cm and the height of the side wall is 5cm.
Calculate the volume of a regular truncated quadrilateral pyramid if the base edges are 10cm and 4cm and the height of the side wall is 5cm. - Axial section
 The diagonal of the axial section of the rotating cylinder is 6 cm, and its surface is 30 cm square. Calculate the radius of the base.
The diagonal of the axial section of the rotating cylinder is 6 cm, and its surface is 30 cm square. Calculate the radius of the base. - Cylinder volume diagonal
 The axial section of the cylinder is a rectangle with a diagonal of u = 20 cm. The height of the cylinder is twice the diameter of the base. Calculate the cylinder volume in liters.
The axial section of the cylinder is a rectangle with a diagonal of u = 20 cm. The height of the cylinder is twice the diameter of the base. Calculate the cylinder volume in liters. - Cone surface volume
 Calculate the cone's surface and volume if its base diameter is 1 dm and the side length is 13 cm.
Calculate the cone's surface and volume if its base diameter is 1 dm and the side length is 13 cm.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
