Pythagorean theorem - math word problems - page 17 of 73
Number of problems found: 1452
- Diagonals
 Given a rhombus ABCD with a diagonal length of 8 cm and 12 cm. Calculate the side length and area of the rhombus.
Given a rhombus ABCD with a diagonal length of 8 cm and 12 cm. Calculate the side length and area of the rhombus. - RT perimeter
 The leg of the rectangular triangle is 7 cm shorter than the second leg and 8 cm shorter than the hypotenuse. Calculate the triangle circumference.
The leg of the rectangular triangle is 7 cm shorter than the second leg and 8 cm shorter than the hypotenuse. Calculate the triangle circumference. - Rhombus OWES
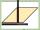 OWES is a rhombus, given that OW is 6cm and one diagonal measures 8cm. Find its area?
OWES is a rhombus, given that OW is 6cm and one diagonal measures 8cm. Find its area? - Chord 5
 It is given a circle k/S; 5 cm /. Its chord MN is 3 cm away from the center of the circle. Calculate its length.
It is given a circle k/S; 5 cm /. Its chord MN is 3 cm away from the center of the circle. Calculate its length. - Rectangle and diagonal
 In the rectangle ABCD, we know the side length is AB = 16 cm, and the diagonal AC = 20 cm. Calculate its perimeter and area.
In the rectangle ABCD, we know the side length is AB = 16 cm, and the diagonal AC = 20 cm. Calculate its perimeter and area. - Chord circle
 The circle to the (S, r = 8 cm) are different points A, B connected segment /AB/ = 12 cm. AB mark the middle of S'. Calculate |SS'|. Make the sketch.
The circle to the (S, r = 8 cm) are different points A, B connected segment /AB/ = 12 cm. AB mark the middle of S'. Calculate |SS'|. Make the sketch. - Length IT
 Find the length (circumference) of an isosceles trapezoid in which the length of the bases a,c, and the height h is given: a = 8 cm c = 2 cm h = 4 cm.
Find the length (circumference) of an isosceles trapezoid in which the length of the bases a,c, and the height h is given: a = 8 cm c = 2 cm h = 4 cm. - Chord 4
 I need to calculate the circumference of a circle, and I know the chord length c=16 cm and the distance from the center d=15 cm chord to the circle.
I need to calculate the circumference of a circle, and I know the chord length c=16 cm and the distance from the center d=15 cm chord to the circle. - RT 11
 Calculate the area of the right triangle if its perimeter is p = 45 m and one cathetus is 20 m long.
Calculate the area of the right triangle if its perimeter is p = 45 m and one cathetus is 20 m long. - Ladder
 10 meters long ladder is leaning against the wall of the well, and its lower end is 1 meters from this wall. How high from the bottom of a well is the top edge of the ladder?
10 meters long ladder is leaning against the wall of the well, and its lower end is 1 meters from this wall. How high from the bottom of a well is the top edge of the ladder? - Diagonals
 Calculate the length of the rhombus's diagonals if its side is long 21 and one of its internal angles is 10°.
Calculate the length of the rhombus's diagonals if its side is long 21 and one of its internal angles is 10°. - Rhombus
 Calculate the length of the diagonal AC of the rhombus ABCD if its perimeter is 524 dm and the other diagonal BD has length 159 dm.
Calculate the length of the diagonal AC of the rhombus ABCD if its perimeter is 524 dm and the other diagonal BD has length 159 dm. - The circle arc
 Calculate the span of the arc, which is part of a circle with diameter d = 11 m and its height is 5 m.
Calculate the span of the arc, which is part of a circle with diameter d = 11 m and its height is 5 m. - Octagon
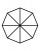 We have a square with a side 56 cm. We cut corners to make his octagon. What will be the side of the octagon?
We have a square with a side 56 cm. We cut corners to make his octagon. What will be the side of the octagon? - Isosceles right triangle
 Calculate the area of an isosceles right triangle whose perimeter is 810 cm.
Calculate the area of an isosceles right triangle whose perimeter is 810 cm. - Triangle 63244
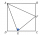 The area of the ABCD square in the picture is 36 cm². Points E and F are the centers of the square BC and CD sides. What is the area of the triangle AEF in cm²?
The area of the ABCD square in the picture is 36 cm². Points E and F are the centers of the square BC and CD sides. What is the area of the triangle AEF in cm²? - Circumference 46171
 Calculate the circumference and area of a rectangle with one side 6 cm long and a diagonal 10 cm long.
Calculate the circumference and area of a rectangle with one side 6 cm long and a diagonal 10 cm long. - Calculate 27441
 Calculate the length of the side of the square if the size of the diagonal u = 9.9 cm is entered.
Calculate the length of the side of the square if the size of the diagonal u = 9.9 cm is entered. - Must-have 7893
 If we want to make a prism with a wooden base with a 5 cm side of a wooden bar, what is the bar's smallest diameter?
If we want to make a prism with a wooden base with a 5 cm side of a wooden bar, what is the bar's smallest diameter? - Calculate: 6686
 We know the right angle γ, side b = 14 cm, and height vc = 8.8 cm in the right triangle ABC. Calculate: angle α = angle β = side a = side c =
We know the right angle γ, side b = 14 cm, and height vc = 8.8 cm in the right triangle ABC. Calculate: angle α = angle β = side a = side c =
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
