Pythagorean theorem - math word problems - page 25 of 73
Number of problems found: 1452
- Chord
 In a circle with a radius r=60 cm is the chord, 4× longer than its distance from the center. What is the length of the chord?
In a circle with a radius r=60 cm is the chord, 4× longer than its distance from the center. What is the length of the chord? - Right-angled 81989
 Using Euclid's Theorems and Pythagoras' Theorem, complete the following parameters describing a right-angled triangle ABC with a right angle at vertex C if we know b=10, cb=8
Using Euclid's Theorems and Pythagoras' Theorem, complete the following parameters describing a right-angled triangle ABC with a right angle at vertex C if we know b=10, cb=8 - Building 81885
 A ladder leans against the building; its length is 7.5 meters. The bottom is 2 meters away from the building. At what height is it leaning against the wall?
A ladder leans against the building; its length is 7.5 meters. The bottom is 2 meters away from the building. At what height is it leaning against the wall? - Rectangular 80776
 The perimeter of the rectangular garden is 42 meters. Its sides are in the ratio 3:4. Calculate the length of the sidewalk that is the diagonal of the garden.
The perimeter of the rectangular garden is 42 meters. Its sides are in the ratio 3:4. Calculate the length of the sidewalk that is the diagonal of the garden. - Isosceles 27793
 The LICH isosceles trapezoid has 5.2 cm long arms and its bases are 7.6 cm and 3.6 cm long. Find the area of the LICH trapezoid.
The LICH isosceles trapezoid has 5.2 cm long arms and its bases are 7.6 cm and 3.6 cm long. Find the area of the LICH trapezoid. - Circumscribed 22713
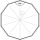 Calculate the circumference and the area of a regular ten-angle polygon if the radius of the circumscribed circle r = 20 cm.
Calculate the circumference and the area of a regular ten-angle polygon if the radius of the circumscribed circle r = 20 cm. - Millimeters 6019
 In an isosceles right triangle, the arms are 50 mm long, and the height at the base is 35.35 mm. Calculate the perimeter of this triangle in millimeters.
In an isosceles right triangle, the arms are 50 mm long, and the height at the base is 35.35 mm. Calculate the perimeter of this triangle in millimeters. - Cross-section 5567
 What diameter must the trunk of a tree have to carve a beam with a square cross-section of 20 cm on it?
What diameter must the trunk of a tree have to carve a beam with a square cross-section of 20 cm on it? - Circumference 5254
 Calculate the shorter side and the diagonal of the rectangle if one side is 2 cm longer than the other and its circumference is equal to 70 centimeters.
Calculate the shorter side and the diagonal of the rectangle if one side is 2 cm longer than the other and its circumference is equal to 70 centimeters. - Rectangle 35
 Find the rectangle area when the diagonal is equal to 30 cm and the width is double the length.
Find the rectangle area when the diagonal is equal to 30 cm and the width is double the length. - Diagonals of rhombus
 Find the length of the diagonal AC of the rhombus ABCD if its perimeter P = 112 dm and the second diagonal BD has a length of 36 dm.
Find the length of the diagonal AC of the rhombus ABCD if its perimeter P = 112 dm and the second diagonal BD has a length of 36 dm. - Michael 2
 Michael has a 35-foot ladder leaning against the side of his house. If the bottom of the ladder is 21 feet away from his house, how many feet above the ground does the ladder touch the house?
Michael has a 35-foot ladder leaning against the side of his house. If the bottom of the ladder is 21 feet away from his house, how many feet above the ground does the ladder touch the house? - Wheel gear
 A drive wheel of radius two is connected to a drive wheel of radius one by a pulley of length 17. What is the distance between the wheel axles?
A drive wheel of radius two is connected to a drive wheel of radius one by a pulley of length 17. What is the distance between the wheel axles? - Triangular land
 Jana has a rectangular garden measuring 30 meters by 72 meters that she wants to split diagonally from corner to corner using a fence. How long does her fence need to be?
Jana has a rectangular garden measuring 30 meters by 72 meters that she wants to split diagonally from corner to corner using a fence. How long does her fence need to be? - Darnell
 Darnell is mountain climbing with Kirk and has just climbed a 9-meter vertical rock face. Kirk is standing at the bottom of the cliff, looking up at Darnell. If Kirk is 15 meters away from Darnell, how far away from the cliff is Kirk standing?
Darnell is mountain climbing with Kirk and has just climbed a 9-meter vertical rock face. Kirk is standing at the bottom of the cliff, looking up at Darnell. If Kirk is 15 meters away from Darnell, how far away from the cliff is Kirk standing? - Flakes
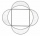 A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips?
A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips? - Constructed triangle
 The perimeter of the right triangle is 18 cm. The sum of the areas of the squares constructed above its three sides is 128 cm². What is the area of the triangle?
The perimeter of the right triangle is 18 cm. The sum of the areas of the squares constructed above its three sides is 128 cm². What is the area of the triangle? - Right triangle eq2
 Find the lengths of the sides and the angles in the right triangle. Given area S = 210 and perimeter o = 70.
Find the lengths of the sides and the angles in the right triangle. Given area S = 210 and perimeter o = 70. - Diagonal 20
 The rectangular town plaza's diagonal pathway is 20 m longer than the width. Suppose the pathway is 20 m shorter than twice the width. How long should the pathway be?
The rectangular town plaza's diagonal pathway is 20 m longer than the width. Suppose the pathway is 20 m shorter than twice the width. How long should the pathway be? - A mast
 The wind broke a mast 32 meters high so that its top touched the ground 16 meters from the pole. The still-standing part of the mast, the broken part, and the ground form a rectangular triangle. At what height was the mast broken?
The wind broke a mast 32 meters high so that its top touched the ground 16 meters from the pole. The still-standing part of the mast, the broken part, and the ground form a rectangular triangle. At what height was the mast broken?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
