Pythagorean theorem - math word problems - page 26 of 73
Number of problems found: 1449
- Sea
 How far can you see from the ship's mast, whose peak is at 9 meters above sea level? (Earth's radius is 6370 km).
How far can you see from the ship's mast, whose peak is at 9 meters above sea level? (Earth's radius is 6370 km). - Determine 23
 Determine in cm² the area of the rectangle ABCD, whose longer side a=20cm and whose diagonal is 10cm longer than its shorter side.
Determine in cm² the area of the rectangle ABCD, whose longer side a=20cm and whose diagonal is 10cm longer than its shorter side. - Right-angled 81019
 In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC.
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC. - Perpendicular 73574
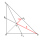 The two lines of the triangle are perpendicular to each other and are 27 cm and 36 cm. Calculate the length of the sides of the triangle and the length of the third line.
The two lines of the triangle are perpendicular to each other and are 27 cm and 36 cm. Calculate the length of the sides of the triangle and the length of the third line. - Hypotenuse 72524
 We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2
We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2 - Perpendicular 67174
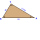 Calculate the perpendicular s in the right triangle STU (the right angle at the vertex U), if the hypotenuse is long u = 93cm and the perpendicular t = 48 cm
Calculate the perpendicular s in the right triangle STU (the right angle at the vertex U), if the hypotenuse is long u = 93cm and the perpendicular t = 48 cm - Right-angled 64084
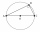 A right-angled triangle ABC with sides 5 cm and 12 cm is described by circle k. Calculate the length of circle k in centimeters. When calculating, use π = 3, 14 and round the result to tenths.
A right-angled triangle ABC with sides 5 cm and 12 cm is described by circle k. Calculate the length of circle k in centimeters. When calculating, use π = 3, 14 and round the result to tenths. - Calculate 47763
 Calculate the area of an isosceles trapezoid ABCD, whose longer base measures 48 cm, the shorter base measures 3/4 of the longest base, and the leg of the trapezoid measures 2/3 of the longer base. The result is rounded to the nearest hundredth.
Calculate the area of an isosceles trapezoid ABCD, whose longer base measures 48 cm, the shorter base measures 3/4 of the longest base, and the leg of the trapezoid measures 2/3 of the longer base. The result is rounded to the nearest hundredth. - Rectangular
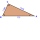 Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K, and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle
Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K, and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle - Isosceles 7929
 ABCD isosceles trapezoid. A = 6cm, e = 7cm and delta angle = 105 °. Calculate the remaining pages.
ABCD isosceles trapezoid. A = 6cm, e = 7cm and delta angle = 105 °. Calculate the remaining pages. - Isosceles 5575
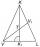 The picture shows an isosceles triangle VLK with a center of gravity of T. The base VL measures 16 cm, and the line KK1 measures 18 cm. How long is the VV1 line?
The picture shows an isosceles triangle VLK with a center of gravity of T. The base VL measures 16 cm, and the line KK1 measures 18 cm. How long is the VV1 line? - Chord AB
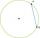 What is the chord AB's length if its distance from the center S of the circle k(S, 50 cm) is 43 cm?
What is the chord AB's length if its distance from the center S of the circle k(S, 50 cm) is 43 cm? - Calculate: 6679
 In the right triangle ABC, we know the right angle γ, the area S = 48 cm2, and the side a = 8 cm. Calculate: pages b, c
In the right triangle ABC, we know the right angle γ, the area S = 48 cm2, and the side a = 8 cm. Calculate: pages b, c - V-belt
 Calculate the length of the belt on pulleys with diameters of 105 mm and 393 mm at shaft distance 697 mm.
Calculate the length of the belt on pulleys with diameters of 105 mm and 393 mm at shaft distance 697 mm. - 2-meter-long 81619
 How tall is the tree if I lean a 2-meter-long ladder against it? The ladder is 0.7 m away from the tree, and the top of the ladder rests against the tree at 2/3 of its height.
How tall is the tree if I lean a 2-meter-long ladder against it? The ladder is 0.7 m away from the tree, and the top of the ladder rests against the tree at 2/3 of its height. - Calculate 73024
 Calculate the permille descent of the railway line in the section of 7.2 km by 21.6 m.
Calculate the permille descent of the railway line in the section of 7.2 km by 21.6 m. - Calculate 6219
 Right triangle. Given: side b = 15.8 angle alpha = 15° 11`. Calculate the side a, c, beta angle, and area.
Right triangle. Given: side b = 15.8 angle alpha = 15° 11`. Calculate the side a, c, beta angle, and area. - Right-angled 5804
 We sorted the lengths of the sides of the two triangles by size: 8 cm, 10 cm, 13 cm, 15 cm, 17 cm, and 19 cm. One of these two triangles is right-angled. Calculate the perimeter of this right triangle in centimeters
We sorted the lengths of the sides of the two triangles by size: 8 cm, 10 cm, 13 cm, 15 cm, 17 cm, and 19 cm. One of these two triangles is right-angled. Calculate the perimeter of this right triangle in centimeters - Circumference 4956
 Calculate the circumference of a diamond whose area is 288cm square and one diagonal is 12.4cm.
Calculate the circumference of a diamond whose area is 288cm square and one diagonal is 12.4cm. - Numerically 4839
 Calculate the diagonal of such a square, which holds that its area is equal to its perimeter (without considering units numerically ...).
Calculate the diagonal of such a square, which holds that its area is equal to its perimeter (without considering units numerically ...).
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
