Pythagorean theorem - math word problems - page 27 of 73
Number of problems found: 1452
- V-belt
 Calculate the length of the belt on pulleys with diameters of 105 mm and 393 mm at shaft distance 697 mm.
Calculate the length of the belt on pulleys with diameters of 105 mm and 393 mm at shaft distance 697 mm. - 2-meter-long 81619
 How tall is the tree if I lean a 2-meter-long ladder against it? The ladder is 0.7 m away from the tree, and the top of the ladder rests against the tree at 2/3 of its height.
How tall is the tree if I lean a 2-meter-long ladder against it? The ladder is 0.7 m away from the tree, and the top of the ladder rests against the tree at 2/3 of its height. - Calculate 73024
 Calculate the permille descent of the railway line in the section of 7.2 km by 21.6 m.
Calculate the permille descent of the railway line in the section of 7.2 km by 21.6 m. - Calculate 6219
 Right triangle. Given: side b = 15.8 angle alpha = 15° 11`. Calculate the side a, c, beta angle, and area.
Right triangle. Given: side b = 15.8 angle alpha = 15° 11`. Calculate the side a, c, beta angle, and area. - Right-angled 5804
 We sorted the lengths of the sides of the two triangles by size: 8 cm, 10 cm, 13 cm, 15 cm, 17 cm, and 19 cm. One of these two triangles is right-angled. Calculate the perimeter of this right triangle in centimeters
We sorted the lengths of the sides of the two triangles by size: 8 cm, 10 cm, 13 cm, 15 cm, 17 cm, and 19 cm. One of these two triangles is right-angled. Calculate the perimeter of this right triangle in centimeters - Circumference 4956
 Calculate the circumference of a diamond whose area is 288cm square and one diagonal is 12.4cm.
Calculate the circumference of a diamond whose area is 288cm square and one diagonal is 12.4cm. - Numerically 4839
 Calculate the diagonal of such a square, which holds that its area is equal to its perimeter (without considering units numerically ...).
Calculate the diagonal of such a square, which holds that its area is equal to its perimeter (without considering units numerically ...). - Determine 4258
 Determine the length of the side of the diamond, with its two diagonals being 12 cm and 6 cm long.
Determine the length of the side of the diamond, with its two diagonals being 12 cm and 6 cm long. - On a mass
 The forces F1, and F2 with magnitudes of 40N act on a mass point M. Their resultant has a magnitude of 60N. Determine the angle that the forces F1 and F2 make.
The forces F1, and F2 with magnitudes of 40N act on a mass point M. Their resultant has a magnitude of 60N. Determine the angle that the forces F1 and F2 make. - Circumscribed circle
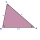 In triangle ABC, we know a = 4 cm, b = 6 cm, γ = 60°. Calculate the area and radius of the inscribed and circumscribed circle.
In triangle ABC, we know a = 4 cm, b = 6 cm, γ = 60°. Calculate the area and radius of the inscribed and circumscribed circle. - The rectangle 5
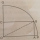 The rectangle OABC has one vertex at O, the center of a circle, and a second vertex, A, 2 cm from the edge of the circle, as shown. The vertex A is also 7 cm from C. The points B and C lie on the circumference of the circle. a. What is the radius? b. Find
The rectangle OABC has one vertex at O, the center of a circle, and a second vertex, A, 2 cm from the edge of the circle, as shown. The vertex A is also 7 cm from C. The points B and C lie on the circumference of the circle. a. What is the radius? b. Find - Right angle
 If b=10, c=6, and c are two sides of a triangle ABC, a right angle is at the vertex A, find the value on each unknown side.
If b=10, c=6, and c are two sides of a triangle ABC, a right angle is at the vertex A, find the value on each unknown side. - A rectangle 2
 A rectangle has a diagonal length of 74cm. Its side lengths are in a ratio of 5:3. Find its side lengths.
A rectangle has a diagonal length of 74cm. Its side lengths are in a ratio of 5:3. Find its side lengths. - Medians in right triangle
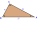 It is given a right triangle, and angle C is 90 degrees. I know it medians t1 = 8 cm and median t2 = 12 cm. How to calculate the length of the sides?
It is given a right triangle, and angle C is 90 degrees. I know it medians t1 = 8 cm and median t2 = 12 cm. How to calculate the length of the sides? - Right isosceles triangle
 The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse, dividing it into two equal segments. One segment is 5 cm long. What is the area of the triangle?
The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse, dividing it into two equal segments. One segment is 5 cm long. What is the area of the triangle? - Bricklayer
 How much do we pay for a bricklayer laying pavement in a square room with a diagonal of 8 m if 1 sqm of work will cost CZK 420?
How much do we pay for a bricklayer laying pavement in a square room with a diagonal of 8 m if 1 sqm of work will cost CZK 420? - Two chords
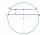 In a circle with a radius of 8.5 cm, two parallel chords are constructed, the lengths of which are 9 cm and 12 cm. Find the distance of the chords in a circle.
In a circle with a radius of 8.5 cm, two parallel chords are constructed, the lengths of which are 9 cm and 12 cm. Find the distance of the chords in a circle. - The mast
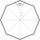 A 40 m high mast is secured in half by eight ropes 25 m long. The ends of the ropes are equidistant from each other. Calculate this distance.
A 40 m high mast is secured in half by eight ropes 25 m long. The ends of the ropes are equidistant from each other. Calculate this distance. - Right triangles
 How many right triangles we can construct from line segments 3,4,5,6,8,10,12,13,15,17 cm long? (Do not forget the triangle inequality).
How many right triangles we can construct from line segments 3,4,5,6,8,10,12,13,15,17 cm long? (Do not forget the triangle inequality). - Height of the arc - formula
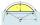 Calculate the arc's height if the arc's length is 65 and the chord length is 33. Does there exist a formula to solve this?
Calculate the arc's height if the arc's length is 65 and the chord length is 33. Does there exist a formula to solve this?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
