Pythagorean theorem - math word problems - page 28 of 73
Number of problems found: 1449
- Calculate 39131
 A circle describes a square with a side of 8 cm. Calculate the area of the rest of the circle if we cut out the square.
A circle describes a square with a side of 8 cm. Calculate the area of the rest of the circle if we cut out the square. - Sidewalk 26121
 The garden has a square shape, and its area is 8,100 m². It will be divided by a sidewalk connecting the two opposite garden peaks. How long will this trail be?
The garden has a square shape, and its area is 8,100 m². It will be divided by a sidewalk connecting the two opposite garden peaks. How long will this trail be? - Hexagon 8167
 How many dm² of organic glass is needed to produce 50 washers in the shape of a regular hexagon? The side is 8 cm long.
How many dm² of organic glass is needed to produce 50 washers in the shape of a regular hexagon? The side is 8 cm long. - Square
 Dan's father has a square of 65.25 milligram square of wire with a diagonal. How will the square be big when one mm weighs 7 mg?
Dan's father has a square of 65.25 milligram square of wire with a diagonal. How will the square be big when one mm weighs 7 mg? - Cosine
 Cosine and sine theorem: Calculate all unknown values (sides and angles) of the triangle ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? °
Cosine and sine theorem: Calculate all unknown values (sides and angles) of the triangle ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? ° - Ratio of squares
 A circle is given, and a square is inscribed. The smaller square is inscribed in a circular arc formed by the square's side and the circle's arc. What is the ratio of the areas of the large and small squares?
A circle is given, and a square is inscribed. The smaller square is inscribed in a circular arc formed by the square's side and the circle's arc. What is the ratio of the areas of the large and small squares? - Irregular pentagon
 A rectangle-shaped, 16 x 4 cm strip of paper is folded lengthwise so that the lower right corner is applied to the upper left corner. What area does the pentagon have?
A rectangle-shaped, 16 x 4 cm strip of paper is folded lengthwise so that the lower right corner is applied to the upper left corner. What area does the pentagon have? - Cable car
 Find the elevation difference of the cable car when it rises by 67 per mille, and the rope length is 930 m.
Find the elevation difference of the cable car when it rises by 67 per mille, and the rope length is 930 m. - Rectangular field
 A rectangular field has a diagonal length of 169m. If the length and width are in the ratio of 12:5. Find the field's dimensions, the field's perimeter, and the field's area.
A rectangular field has a diagonal length of 169m. If the length and width are in the ratio of 12:5. Find the field's dimensions, the field's perimeter, and the field's area. - Diagonals of the rhombus
 How long are the diagonals e, and f in the diamond if its side is 5 cm long and its area is 20 cm²?
How long are the diagonals e, and f in the diamond if its side is 5 cm long and its area is 20 cm²? - Ladder
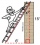 Adam placed the ladder of the house, the upper end reaching the window at the height of 3.6m, and the lower end standing on level ground and distant from a wall of 1.5m. What is the length of the ladder?
Adam placed the ladder of the house, the upper end reaching the window at the height of 3.6m, and the lower end standing on level ground and distant from a wall of 1.5m. What is the length of the ladder? - Surveyor
 Calculate the area of what may vary rectangular if it was focused by a surveyor and found the dimensions 10 x 16 m while in each of the four joint points can be position deviation 8 cm?
Calculate the area of what may vary rectangular if it was focused by a surveyor and found the dimensions 10 x 16 m while in each of the four joint points can be position deviation 8 cm? - Rhombus
 It is given a rhombus with a side length of a = 20 cm. Touchpoints of the inscribed circle divided its sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus.
It is given a rhombus with a side length of a = 20 cm. Touchpoints of the inscribed circle divided its sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus. - Right
 Determine angles of the right triangle with the hypotenuse c and legs a, b, if: 2a +5b = 5.283c
Determine angles of the right triangle with the hypotenuse c and legs a, b, if: 2a +5b = 5.283c - Trapezoid
 Trapezoid ABCD a = 35 m, b=28 m c = 11 m and d = 14 m. How to calculate its area?
Trapezoid ABCD a = 35 m, b=28 m c = 11 m and d = 14 m. How to calculate its area? - Diagonals 82850
 How do I find the diagonals of a rhombus if its perimeter is 80dm and one diagonal is 2x larger than the other?
How do I find the diagonals of a rhombus if its perimeter is 80dm and one diagonal is 2x larger than the other? - Calculate 70804
 The garden is a right triangle fenced with a 364 m fence length. The shorter slope of the triangle is 26 m long. Calculate the area of this garden.
The garden is a right triangle fenced with a 364 m fence length. The shorter slope of the triangle is 26 m long. Calculate the area of this garden. - Centimeter 64224
 A ladder leans against the wall. It touches the wall at the height of 340 cm, and its lower end is 160 cm away from the wall. How long is the ladder? Express the result to the nearest centimeter.
A ladder leans against the wall. It touches the wall at the height of 340 cm, and its lower end is 160 cm away from the wall. How long is the ladder? Express the result to the nearest centimeter. - Cross-section 23491
 The cross-section of the railway embankment is an isosceles trapezoid, the bases of which are in a ratio of 5:3. The arms have a 5 m embankment height v = 4.8 m. Calculate the section area S.
The cross-section of the railway embankment is an isosceles trapezoid, the bases of which are in a ratio of 5:3. The arms have a 5 m embankment height v = 4.8 m. Calculate the section area S. - The sides 2
 The sides of a trapezoid are in the ratio 2:5:8:5. The trapezoid's area is 245. Find the height and the perimeter of the trapezoid.
The sides of a trapezoid are in the ratio 2:5:8:5. The trapezoid's area is 245. Find the height and the perimeter of the trapezoid.
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
